Предмет: Алгебра,
автор: yvyvgvyvyvgv5567
найти производную/знайти похідну
Приложения:
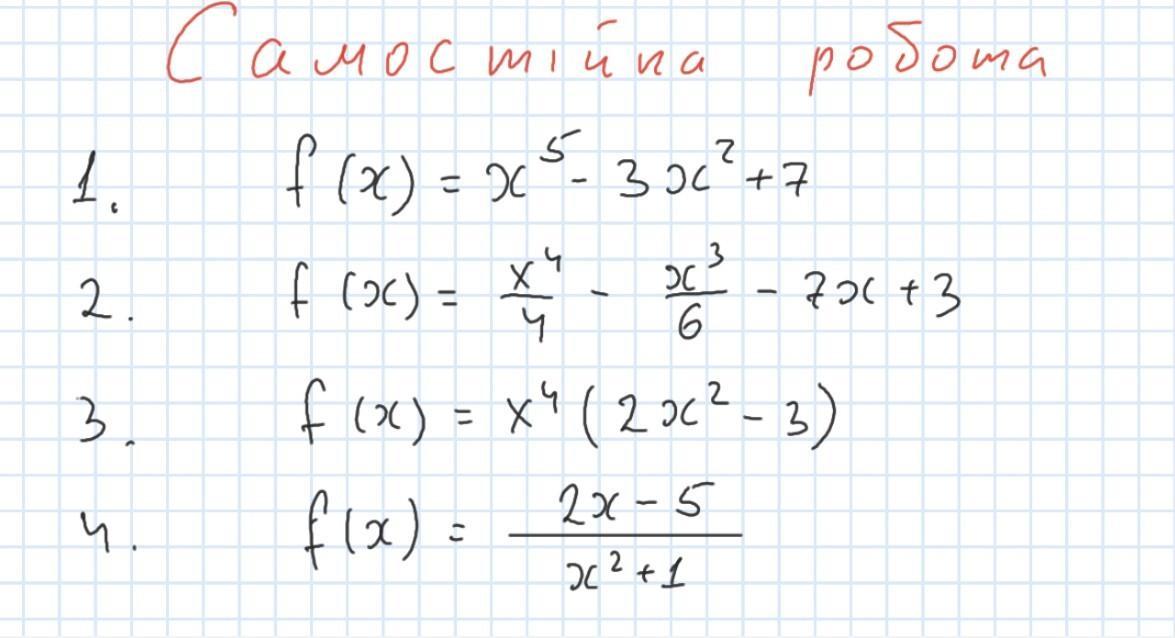
Ответы
Автор ответа:
2
1)
2)
3)
4)
Похожие вопросы
Предмет: Физика,
автор: karolinkapisar
Предмет: Английский язык,
автор: hinkiz
Предмет: Химия,
автор: pacadzid
Предмет: Русский язык,
автор: malikavip9