r=3
R=5
KM=2корень из 15
Касаются ли окружности?

Ответы
Ответ:
Нет, окружности не касаются. Радиусы окружностей не пересекаются и не пересекаются с точкой соприкосновения, так как они не удовлетворяют условию теоремы о треугольниках с прямым углом: a² + b² = c², где a и b – радиусы окружностей, а c – расстояние между центрами окружностей. В данном случае расстояние между центрами окружностей равно |3 - 5| = 2, что больше 2√15, поэтому они не касаются.
Объяснение:
Пусть расстояние между центрами равно сумме радиусов.
Тогда на отрезке O₁O₂ есть точка P, удаленная от центра каждой окружности на её радиус - общая точка двух окружностей.
Предположим, существует вторая общая точка Q не на отрезке O₁O₂. Тогда ломанная O₁QO₂ длиннее суммы радиусов, что невозможно.
Итак: если расстояние между центрами равно сумме радиусов, то окружности имеют одну общую точку на линии центров, т.е. касаются внешним образом.
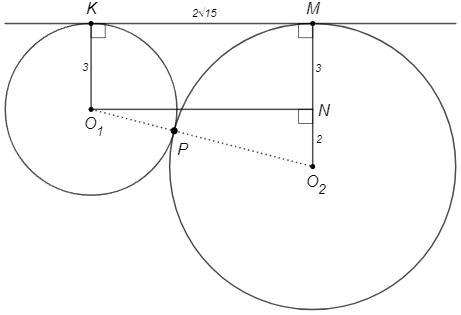
O1K⊥KM, O2M⊥KM (радиусы в точку касания), O1N⊥O2M
=> O1KMN - прямоугольник
O1N=KM=2√15
MN=O1K=3 => O2N=O2M-MN =2
O1O2 =√(O1N^2+O2N^2) =√(4*15+4) =8
Расстояние между центрами O₁O₂ равно сумме радиусов (5+3), следовательно окружности касаются внешним образом.