Question

СРОЧНО, ПЕШИТЕ ПОЖАЛУЙСТА!!!

З точки до площини прямокутної трапеції з основами 2N см і N см та більшою бічної сторони N √2 проведено перпендикуляр з основою у вершині гострого кута. Відстань від даної точки
До протилежної вершини трапеції дорівнює N √6
Знайти відстань від цієї точки до площини трапеції

Answer 1

Ответ:

Расстояние от точки до плоскости трапеции равно N.

Объяснение:

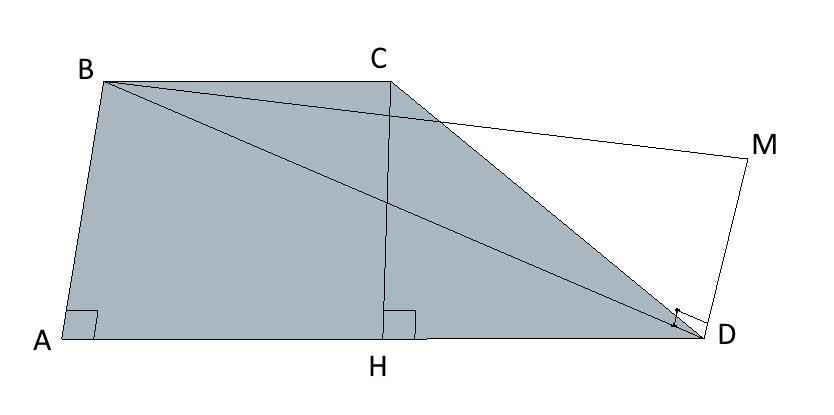
С точки к плоскости прямоугольной трапеции с основаниями 2N см и N см и большей боковой стороны N√2 проведен перпендикуляр с основанием в вершине острого угла. Расстояние от данной точки до противоположной вершины трапеции равно N√6. Найти расстояние от этой точки до плоскости трапеции.

AD = 2N

BC = N

CD = N√2

MB = N√6

∠BAD = 90°

MD ⊥ ABCD

MD - ?

——————————————

Проведем высоту CH, она будет равна стороне AB, при этом BC = AH, тогда HD = AD-AH = 2N-N = N.

Из треугольника CDH по т. Пифагора найдем CH:

AB = CH = √(CD²-HD²) = √((N√2)²-N²) = √N² = N

Из прямоугольного треугольника ABD найдем BD:

BD = √(AD²+AB²) = √((2N)²+N²) = √(5N²) = N√5

Из прямоугольного треугольника MBD найдем MD:

MD = √(MB²-BD²) = √((N√6)²-(N√5)²) = √N² = N