Предмет: Алгебра,
автор: dullakki
10. Найдите производную функции f(x)=√3x+1, пользуясь определением производной.
Формулу (√U)' = 1/2√U * U' не предлагать!!!!
Приложения:
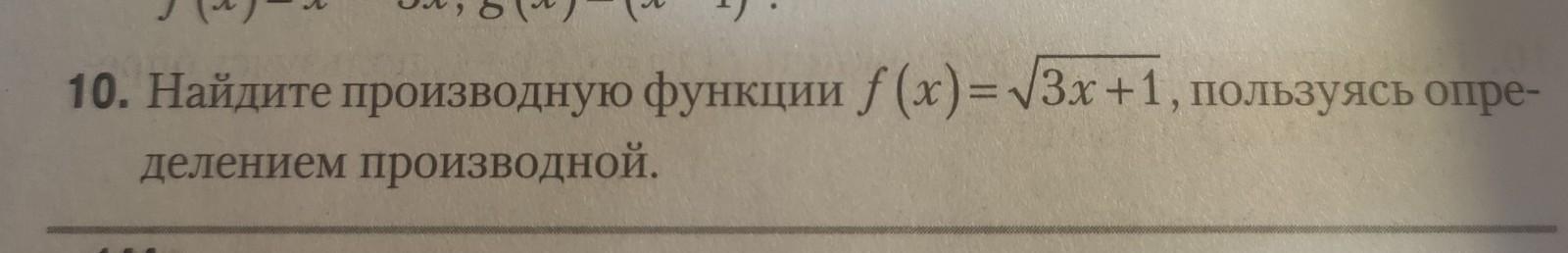
Ответы
Автор ответа:
1
dullakki:
Мне кажется избавляться от иррациональности в знаменателе это лишнее для производной
Пожалуйста реши через ∆f/∆x
возможно и не стоит избавляться от иррациональности в знаменателе, дело првычки
вам решить задачу через придел нужно?
∆f/∆x-?
Похожие вопросы