В правильный треугольник ABC со стороной 12 см вписанна окружность и проведена вторая окружность с центром в точке С и радиусом 6 см . Найдите площадь общей части полученных кругов.
Ответы
Объяснение:
Пусть O - центр вписанной окружности треугольника ABC, а R - радиус этой окружности. Так как треугольник ABC правильный, то его центр описанной окружности совпадает с центром вписанной окружности и лежит на пересечении медиан. Поэтому CO является медианой и высотой треугольника ABC.
Таким образом, CO = 1/2 * AB = 1/2 * 12 = 6 см.
Также заметим, что обе окружности касаются стороны AB треугольника ABC, поэтому точка касания между ними будет серединой стороны AB.
Пусть M - середина стороны AB. Тогда AM = MB = 6 см.
Так как радиус второй окружности равен 6 см, то её центр лежит на пересечении медиан треугольника ABC.
Таким образом, точки O, C и центр второй окружности лежат на одной прямой.
Рассмотрим треугольники COA и CEB, где E - точка касания второй окружности со стороной BC треугольника ABC. Эти треугольники равнобедренные, так как OC является высотой треугольника ABC и проходит через центры окружностей O и C.
Таким образом, угол COA равен углу CEB, а угол OCA равен углу ECB.
Значит, треугольники COA и CEB подобны, поэтому отношение сторон CO и CE равно отношению сторон OA и EB.
CO/CE = OA/EB
6/6 = R/(R+6)
R = 12 см
Таким образом, площадь общей части полученных кругов равна сумме площадей двух секторов окружности с радиусом 12 см и центром O и разности площадей треугольника ABC и треугольника, образованного отрезком CE и дугой второй окружности.
S = 1/3 * π * R^2 + 1/3 * π * R^2 - 1/2 * CE * R + 1/2 * CE * (R+6)
S = 1/3 * π * 12^2 + 1/3 * π * 12^2 - 1/2 * 6 * 12 + 1/2 * 6 * 18
S = 144π/3 - 36
S = 48π - 36
S ≈ 98.68 см²
Ответ:
Объяснение:
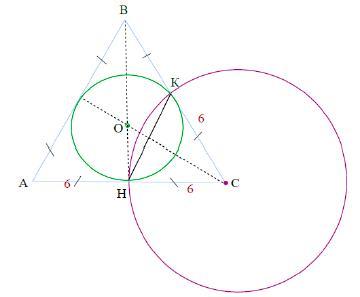
1) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
Но так как в равностороннем Δ-ке биссектрисы, медианы и высоты совпадают, то центр вписанной в правильный треугольник окружности является точкой пересечения как его биссектрис, так и медиан и высот.
В равностороннем Δ-ке все медианы (высоты, биссектрисы) равны.
Поскольку медианы делят сторону пополам, то
АН =НС = СК =КВ = ... = 12/2 = 6(см)
2) Так как центр окружности лежит на пересечении медиан Δ-ка, а медианы в точке пересечения делятся в отношении 2:1, то считая от вершины, то радиус вписанной окружности равен одной третьей длины медианы:
R₁ = ОН = ВН/3
ВН = АВ *sin 60° (т.к. все углы в равностороннем Δ-ке равны)
ВН = 12*√3/2 = 6√3
R₁ = 6√3/3
R₁ = 2√3
3) Окружность с центром в т.С будет проходить через т.Н и т.К, т.к. её радиус R₂ = 6см = СН =СК
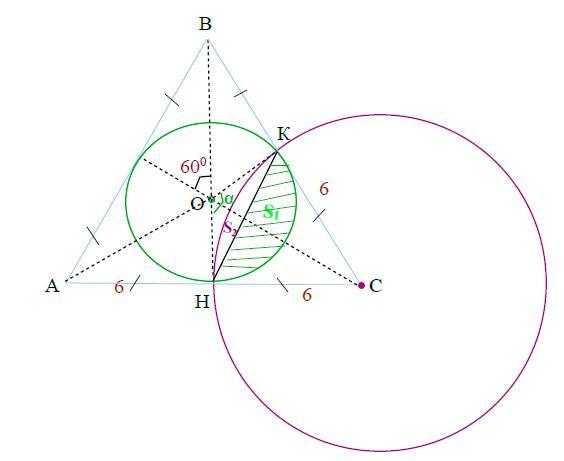
4) Чтобы найти площадь общей части полученных кругов можно найти площади секторов S₁ и S₂ и затем сложить их.
5) Площадь сегмента S₁ равна разности площадей кругового сектора КОН и ΔКОН. В случае, когда величина α выражена в градусах, формула следующая:
S₁ = πR₁²α/360° - ¹/₂R₁² sinα = ¹/₂R₁²(πα/180° - sinα)
Т.к. ΔАВС - равносторонний, все его медианы (высоты и биссектрисы) делят этот Δ-к на 6 равных Δ-ков. Тогда угол между медианами будет равен 90° – 60° :2 = 90° – 30° = 60°.
∠α = 2*60° =120°, тогда
S₁ = ¹/₂ (2√3)² (π*120°/180° - sin120°) = 2*3 = 6(2π/3 - √3/2)
S₁ = 6(2π/3 - √3/2) =
S₁ = 4π -3√3
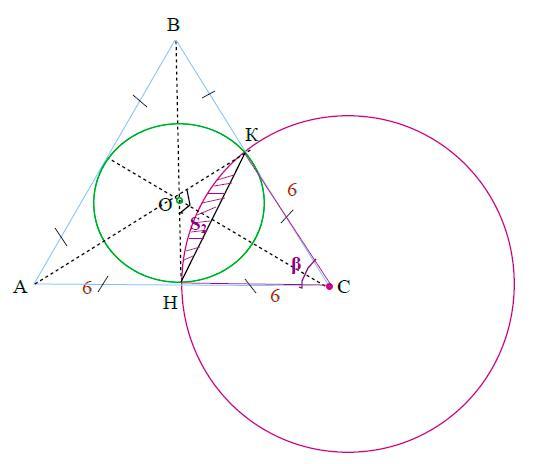
6) Аналогично, площадь сегмента S₂ равна разности площадей кругового сектора КCН и ΔКCН
S₂ = ¹/₂R₂²(πα/180° - sinβ)
R₂ = 6см
Т.к. сумма углов 4-хугольника ОКСН = 360°, а
∠КОН =120°, ∠ОКС = ∠ОНС = 90°, то
∠КСН = ∠β = 360°-180° -120° = 60°.
Получим:
S₂ = ¹/₂ * 6²(π60°/180° - sin60°) = 18(π/3 - √3/2)
S₂ = 6π - 9√3
S = S₁ + S₂ = 4π -3√3 + 6π - 9√3 = 10π - 12√3
Ответ: площадь общей части полученных кругов равна: 10π - 12√3