Предмет: Математика,
автор: rkia978
Знатоки математики, помогите, пожалуйста!
Нужно решение)
Очень срочно ...
Приложения:
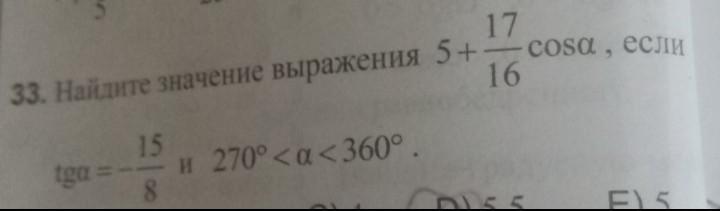
Ответы
Автор ответа:
2
ответ на прикрепленной фотографии
Приложения:

Автор ответа:
2
Найдём соs через тригонометрическое тождество:
Т.к. 270° < а < 360° (4 четверть), то cos будет положительным:
Подставим значение cos в выражение:
Похожие вопросы
Предмет: Геометрия,
автор: starodynovakarina41
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: misak3394
Предмет: Математика,
автор: eduard4067