Предмет: Геометрия,
автор: Artherium
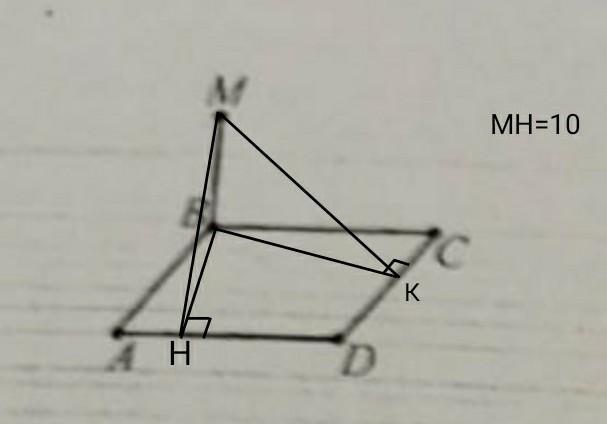
M 8. ABCD параллелограмм, МВ L АВС, MB = 8, d (M, AD) = 10, AD = 20, DC = 8. Найдите d (M, DC).
Приложения:

Ответы
Автор ответа:
2
Ответ:
MK=17 ед
Объяснение:
МН=10 (d(M;AD))
∆МНВ- прямоугольный треугольник.
По теореме Пифагора:
ВН=√(МН²-МВ²)=√(10²-8²)=6 ед.
S(ABCD)=BH*AD;
S(ABCD)=BK*DC;
BH*AD=BK*DC; →
BK=BH*AD/DC=6*20/8=15 ед
∆МВК- прямоугольный треугольник.
По теореме Пифагора:
МК=√(МВ²+ВК²)=√(8²+15²)=√(64+225)=
=√289=17 ед (d(M;DC))
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: candy102992
Предмет: Английский язык,
автор: ipolyansjka
Предмет: Физика,
автор: supergirl81
Предмет: История,
автор: lolita6493