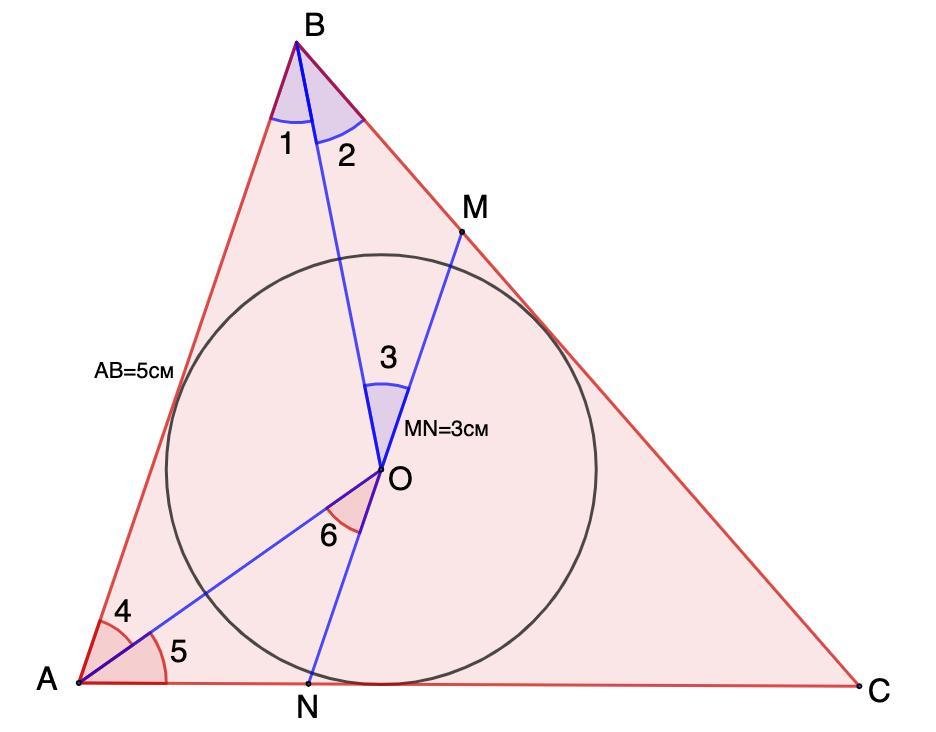
Через центр кола, вписаного в трикутник АВС, провели пряму MN паралельно стороні АВ (точки М i N належать відповідно сторонам ВС і АС). Знайдіть периметр чотири- кутника АВMN, якщо відомо, що АВ = 5 см, MN = 3 см.
Ответы
Ответ:
Периметр четырехугольника АВMN равен 11 см.
Объяснение:
Через центр окружности, вписанной в треугольник АВС, провели прямую MN параллельно сторонам АВ (точки M и N принадлежат соответственно сторонам ВС и АС). Найдите периметр четырехугольника AВMN, если известно, что AВ = 5 см, MN = 3 см.
Дано: ΔАВС;
Окр.О - описана около ΔАВС;
О ∈ MN;
MN || AB;
AB = 5 см; MN = 3 см.
Найти: Р(АВMN)
Решение:
Обозначим углы цифрами для удобства.
- Периметр - сумма длин всех сторон четырехугольника.
АВ = 5 см; MN = 3 см.
Надо найти ВМ и AN.
- Центр вписанной окружности лежит на биссектрисе угла.
⇒ ВО - биссектриса ∠В; АО - биссектриса ∠А.
Тогда:
∠1 = ∠2; ∠4 = ∠5.
MN || AB
- При пересечении двух параллельных прямых секущей, накрест лежащие углы равны.
⇒ ∠1 = ∠3 (накрест лежащие при MN || AB и секущей ВО)
∠4 = ∠6 (накрест лежащие при MN || AB и секущей АО)
⇒ ∠2 = ∠3; ∠5 = ∠6.
Рассмотрим ΔОВМ.
∠2 = ∠3
- Если в треугольнике два угла равны, то этот треугольник равнобедренный.
⇒ ВМ = МО.
Рассмотрим ΔАОN.
∠5 = ∠6
⇒ ΔАОN - равнобедренный.
АN = NO
P(ABMN) = AB + MN + BM + AN = AB + MN + MO + NO =
= AB + MN +MN = 5 + 3 + 3 = 11 (см)
Периметр четырехугольника АВMN равен 11 см.
#SPJ1