Question

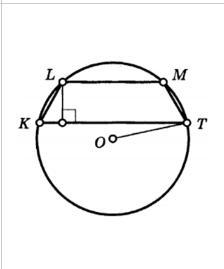
По данным на рисунке найдите радиус описанной окружности ОТ около трапеции KLMT, если LM = 12, KT = 16 и высота трапеции равна 2.

Answer 1

Ответ:

10.

Объяснение:

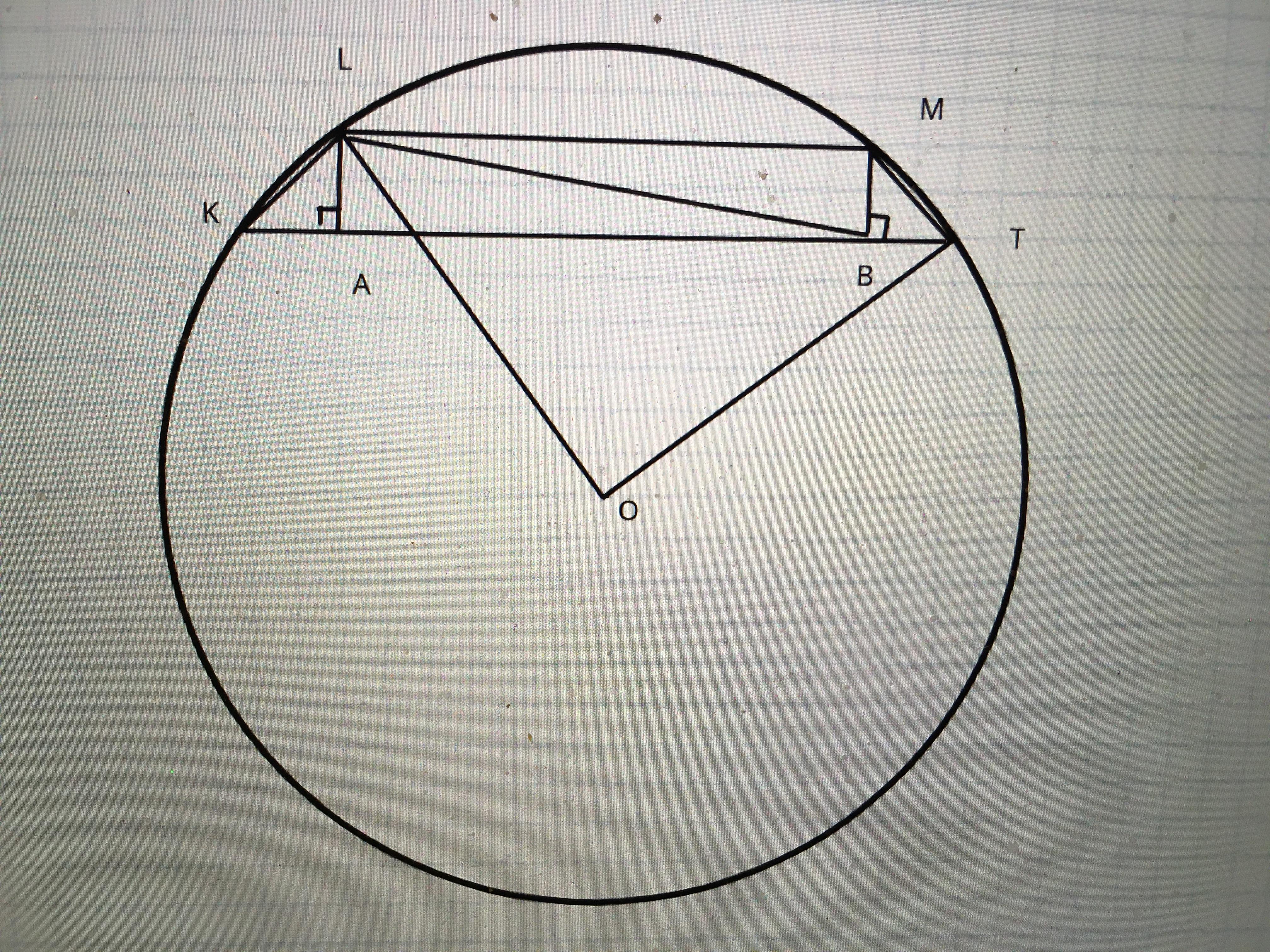
Поскольку трапеция вписана в окружность, она равнобокая, а тогда

               $KA=TB=\dfrac{KT-AB}{2}=\dfrac{KT-LM}{2}=\dfrac{16-12}{2}=2,$

а поскольку LA по условию равна 2, треугольник KLA равнобедренный прямоугольный, откуда угол LKA равен 45°. Далее из прямоугольного треугольника LTA по теореме Пифагора находим

                            $LT=\sqrt{2^2+14^2}=\sqrt{200}=10\sqrt{2}.$

Далее находим радиус описанной окружности или с помощью теоремы синусов, примененной к треугольнику KLT:

                           $\dfrac{LT}{\sin LKT}=2R;\ \dfrac{10\sqrt{2}}{\sqrt{2}/2}=2R;\ R=10,$

или из треугольника LOT: LO=TO=R; угол LOT = 90° (это следует из того, что вписанный угол LKT равен 45°, а центральный угол LOT опирается на ту же дугу и поэтому в 2 раза больше угла LKT), поэтому треугольник LOT равнобедренный прямоугольный с гипотенузой $LT=10\sqrt{2}\Rightarrow R=OT=10.$