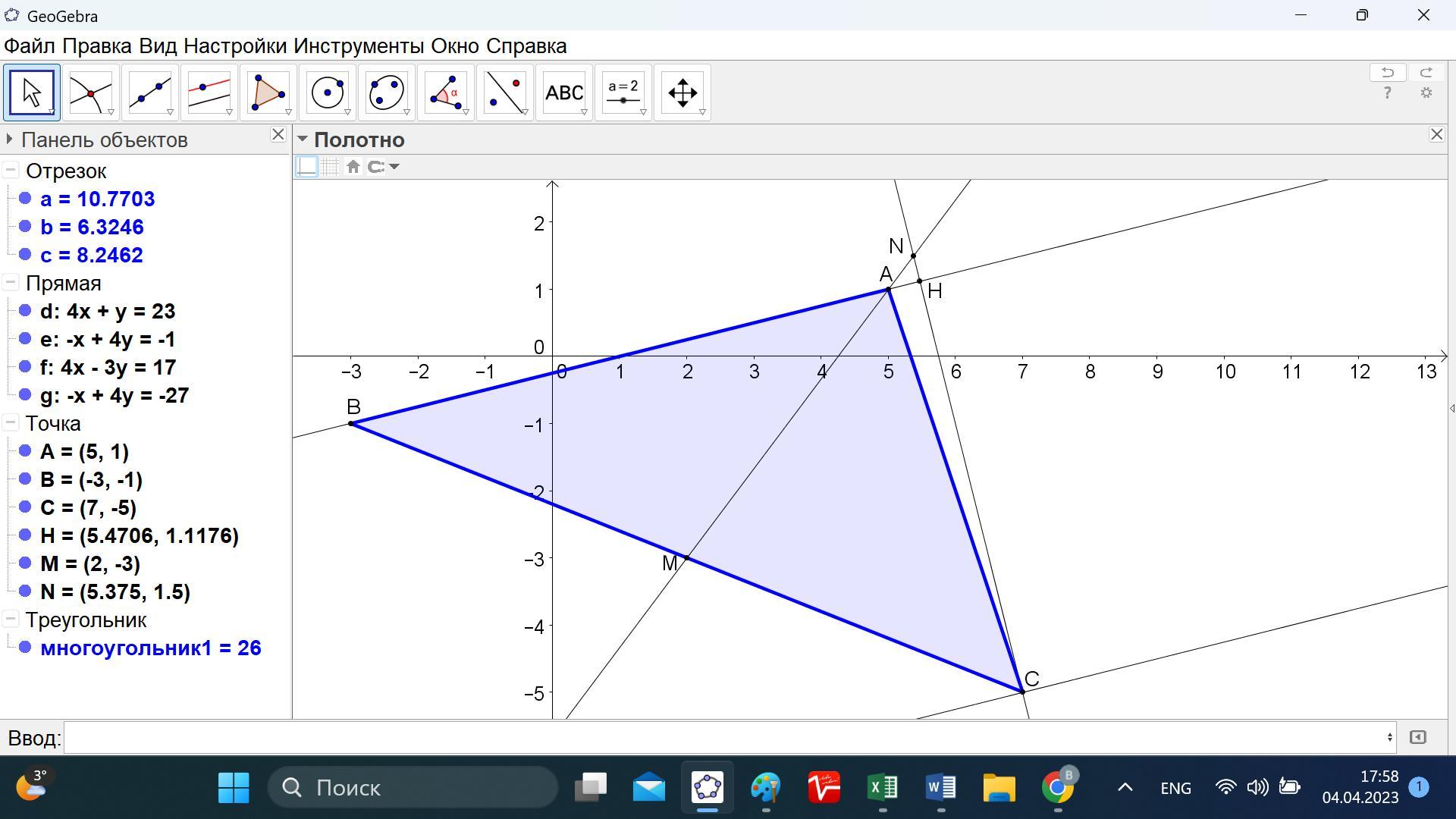
Даны вершины треугольника АВС: A(5; 1); B(-3; -1); C(7; -5)
Найти:
а) уравнение стороны AB;
б) уравнение высоты CH;
в) уравнение медианы AM;
г) точку N персечения медианы AM и высоты CH;
д) уравнение прямой, проходящей через вершину C параллельно стороне AB;
е) расстояние от точки C до прямой AB
Ответы
Даны вершины треугольника АВС: A(5; 1); B(-3; -1); C(7; -5)Найти:
а) уравнение стороны AB.
Находим вектор АВ.
АВ = B(-3; -1) - A(5; 1) = (-8; -2).
Уравнение АВ:
(x – 5)/(-8) = (y – 1)/(-2) каноническое,
-2х + 10 = -8у + 8,
2х- 8у – 2 = 0 или х – 4у – 1 = 0 общее,
у = (1/4)х – (1/4) с угловым коэффициентом (к = (1/4)).
б) уравнение высоты CH.
В общем виде Ах + Ву + С = 0 в уравнении перпендикулярной прямой коэффициенты А и В меняются на (-А) и В или А и (-В).
Высота СН это перпендикуляр к прямой АВ: х – 4у – 1 = 0.
Получаем уравнение СН: 4х + у + С = 0.
Для определения коэффициента С подставим координаты точки С(7; -5), через которую проведен перпендикуляр
4*7 + (-5) + С = 0, отсюда С = 5 – 28 = -23.
Уравнение СН: 4х + у - 23 = 0.
в) уравнение медианы AM.
Находим координаты точки М как середину стороны ВС.
М = (B(-3; -1) + C(7; -5))/2 = (2; -3).
Вектор АМ = (2 – 5; -3 – 1) = (-3; -4).
Уравнение АМ: (х – 5)/(-3) = (у – 1)/(-4),
-4x + 20 = -3y + 3,
4x – 3y – 17 = 0.
г) точку N пересечения медианы AM и высоты CH.
Для этого надо решить систему:
{4x – 3y – 17 = 0
{4х + у - 23 = 0.
-4y + 6 = 0,
y = 6/4 = 1,5.
х = (3y + 17)/4 = (3*1,5 + 17)/4 = 21,5/4 = 5,375.
Точка N = (5,375; 1,5).
д) уравнение прямой, проходящей через вершину C параллельно стороне AB.
Коэффициенты сохраняются, как и у прямой АВ: х – 4у – 1 = 0.
х – 4у + С = 0.
Для определения слагаемого С подставим координаты точки С(7; -5.
7 – 4* (-5) + С = 0, отсюда С = -7 – 20 = -27.
Получаем уравнение: х – 4у - 27 = 0.
е) расстояние от точки C до прямой AB.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C|/√(A² + B²)
Подставим в формулу данные:
d = |1·7 + (-4)·(-5) + (-1)| /√(1² + (-4)²) = |7 + 20 - 1|/√(1 + 16) =
= 26/√17 = 26√17/17 ≈ 6,3059.