Предмет: Алгебра,
автор: masha01021
Помогите пожалуйста решить задачу
Приложения:
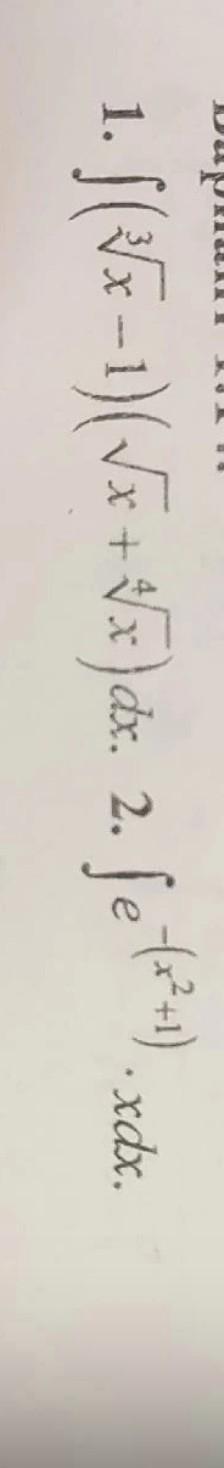
Ответы
Автор ответа:
1
Ответ:
1.
2.
Объяснение:
Вычислить интеграл:
1.
2.
1.
Упростим подинтегральное выражение:
Теперь можем воспользоваться формулой интеграла степенной функции:
2.
Замена переменной:
Получим интеграл:
И обратная замена:
masha01021:
огромное спасибо
Похожие вопросы
Предмет: Литература,
автор: dianazhanibekova94
Предмет: Физика,
автор: ulabulic68
Предмет: Геометрия,
автор: R1verUA
Предмет: Геометрия,
автор: hamibullahabibullaev