Question

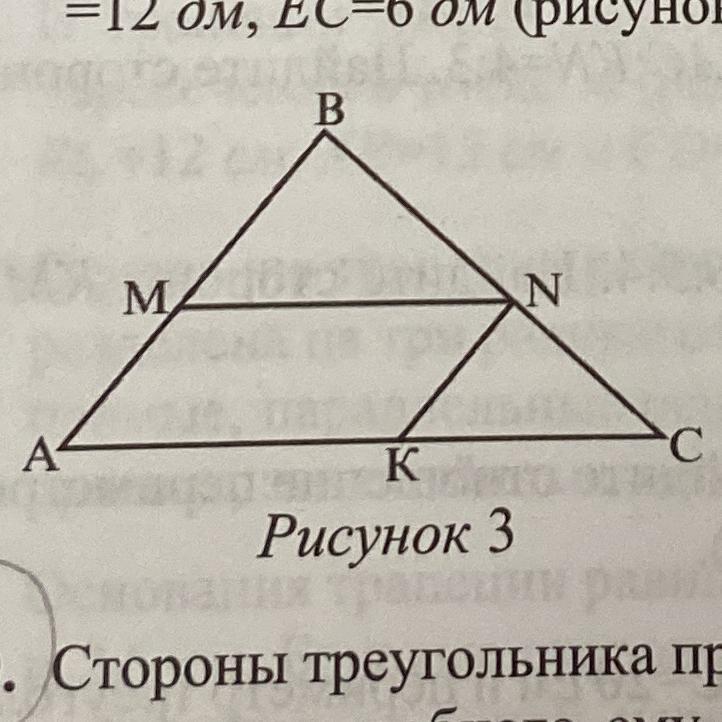
14. В треугольнике ABC, MN||AC, NK||AB, AM:MN=1:3, AB=8 см, AC-
=15 см. Найдите периметр четырёхугольника АMNK (рисунок 3).

Answer 1

Ответ:

23.

Пошаговое объяснение:

Пошаговое объяснение:

В треугольнике ABC с параллельными сторонами MN и AC и NK и AB, где AM:MN = 1:3, AB = 8 см и AC = 15 см. Поскольку MN параллельна AC и AM:MN = 1:3, то AN:NC = 1:3. Таким образом, AN = (1/4) * AC = (1/4) * 15 см = 3.75 см и NC = AC - AN = 15 см - 3.75 см = 11.25 см.

Так как NK параллельна AB, то AK:KB = AN:NC = 1:3. Следовательно, AK = (1/4) * AB = (1/4) * 8 см = 2 см и KB = AB - AK = 8 см - 2 см = 6 см.

Теперь мы можем найти длины сторон MN и NK. MN = (3/4) * AC = (3/4) * 15 см = 11.25 см и NK = (3/4) * AB = (3/4) * 8 см = 6 см.

Периметр четырёхугольника АMNK равен AM + MN + NK + KA = AN + MN + NK + KA = 3.75 см + 11.25 см + 6 см + 2 см = 23 см.