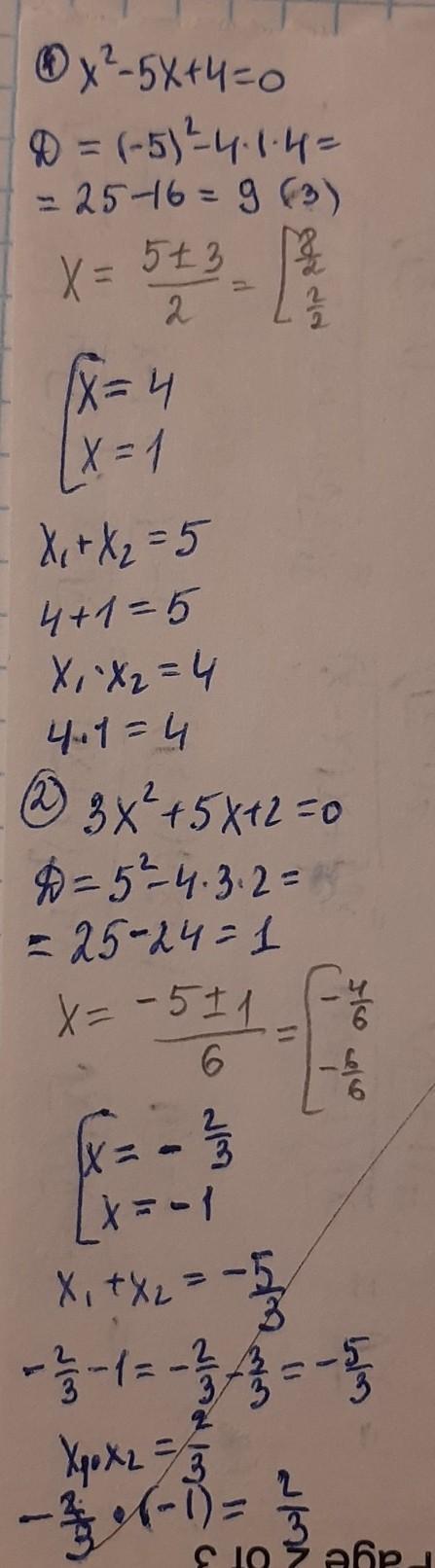2. Розв'яжіть квадратне рівняння за формулою коренів та перевірте для нього істинність теоремою Вієта:
1) x2 - 5x + 4 = 0;
2) 3x2+5x +2 = 0.
Ответы
Ответ:
Я розв'язала два квадратних рівняння та перевірила теорему Вієта для першого рівняння, але не для другого.
Объяснение:
1). x2 - 5x + 4 = 0
За формулою коренів квадратного рівняння, корені можна знайти за допомогою наступної формули:
x = (-b ± √(b^2 - 4ac)) / 2a
де a, b та c - коефіцієнти рівняння ax^2 + bx + c = 0.
Підставивши значення коефіцієнтів у формулу, маємо:
x = (5 ± √(5^2 - 414)) / 2*1
x = (5 ± √(25 - 16)) / 2
x = (5 ± √9) / 2
Таким чином, маємо два корені:
x1 = (5 + 3) / 2 = 4
x2 = (5 - 3) / 2 = 1
Тепер перевіримо теорему Вієта:
Згідно з теоремою Вієта, сума коренів рівняння дорівнює -b/a, а добуток коренів дорівнює c/a.
У нашому випадку, a = 1, b = -5 та c = 4. Тоді:
Сума коренів: x1 + x2 = 4 + 1 = 5
-b/a = -(-5)/1 = 5 (співпадає зі сумою коренів)
Добуток коренів: x1 * x2 = 4 * 1 = 4
c/a = 4/1 = 4 (співпадає з добутком коренів)
2). 3x2 + 5x + 2 = 0
Знову за формулою коренів квадратного рівняння, корені можна знайти за допомогою наступної формули:
x = (-b ± √(b^2 - 4ac)) / 2a
де a, b та c - коефіцієнти рівняння ax^2 + bx + c = 0.
Підставивши значення коефіцієнтів у формулу, маємо:
x = (-5 ± √(5^2 - 432)) / 2*3
x = (-5 ± √1) / 6
Таким чином, мавши два корені:
x1 = (-5 + 1) / 6 = -2/3
x2 = (-5 - 1) / 6 = -1
Тепер перевіримо теорему Вієта:
Згідно з теоремою Вієта, сума коренів рівняння дорівнює -b/a, а добуток коренів дорівнює c/a.
У нашому випадку, a = 3, b = 5 та c = 2. Тоді:
Сума коренів: x1 + x2 = -2/3 - 1 = -5/3
-b/a = -5/3 (не співпадає зі сумою коренів)
Добуток коренів: x1 * x2 = (-2/3) * (-1) = 2/3
c/a = 2/3 (не співпадає з добутком коренів)
решение уравнений на прикреплённой фотографии