ПОМОГИТЕ ПОЖАЛУЙСТА, СРОЧНО!
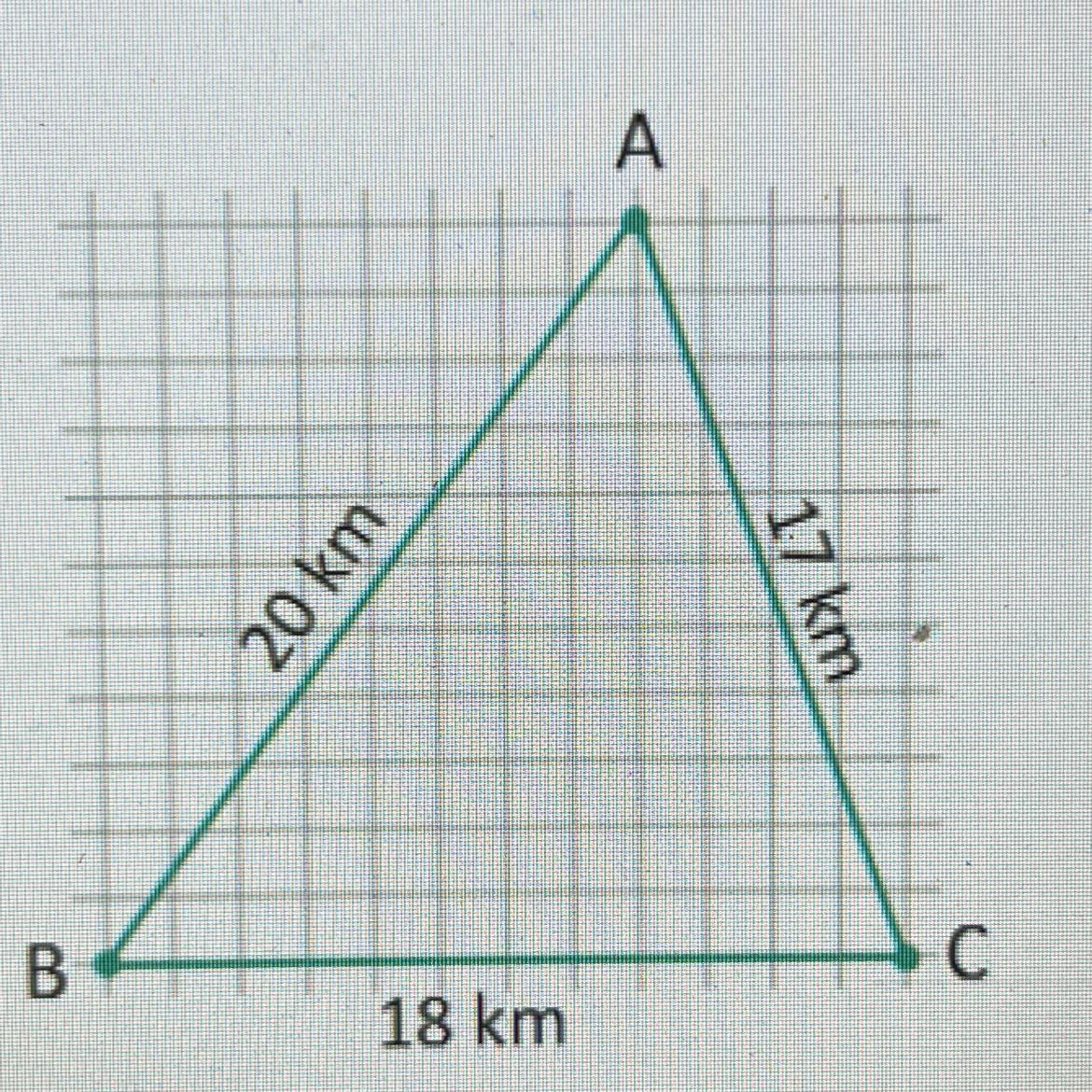
Три школы A, B и C,
расположенные по заданному плану, хотят построить общий теннисный корт. Каждая школа хочет, чтобы теннисный корт находился не дальше 10 км от него. Можно ли выбрать место для теннисного корта, соблюдая это условие? Создайте соответствующий рисунок, следуя масштабу.
Ответы
Відповідь:
Соблюдая это условие выбрать место для теннисного корта нельзя.
Покрокове пояснення:
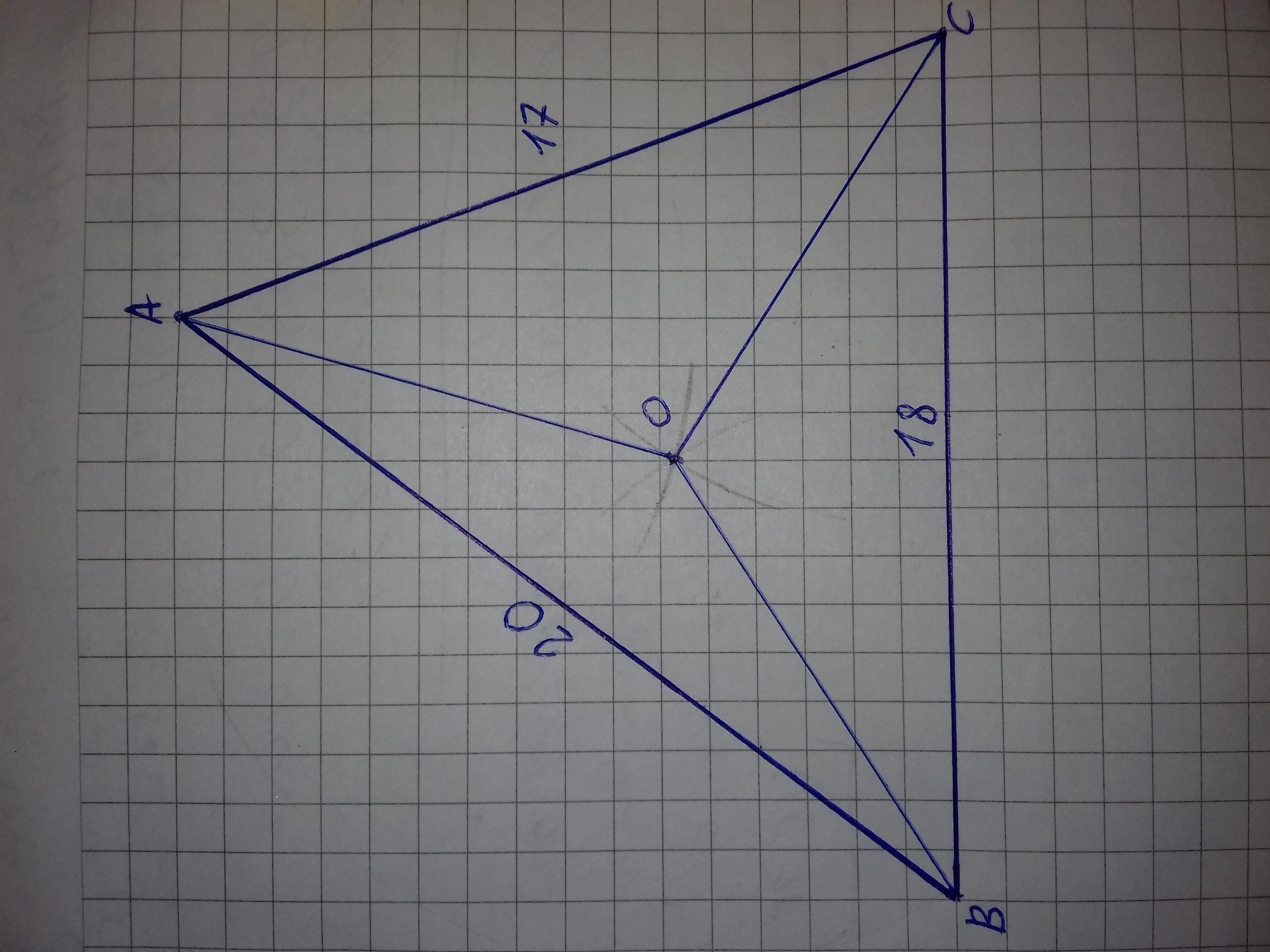
Так, как, сторона АВ треугольника АВС равна 20 км., то даже если теннисный корт будет расположен по середине отрезка АВ, то расстояние от него до школ А и В будет равно 20 / 2 = 10 км. При этом расстояние до школы С будет больше 10 км. Для того, что бы расстояние от середины отрезка АВ до точки С было равно 10 км. угол С треугольника АВС должен быть равен 90° ( это свойство окружности, описанной около прямоугольного треугольника ), а он меньше 90° - это видно даже визуально.
Найдем радиус описанной около треугольника АВС окружности, её центр - это и будет точка, равноудаленная от точек А, В и С.
АВ = а = 20 км.
ВС = в = 18 км.
СА = с = 17 км.
Полупериметр треугольника АВС равен:
р = ( а + в + с ) / 2 = ( 20 + 18 + 17 ) / 2 = 55 / 2 = 27,5 км.
Радиус описанной около треугольника АВС окружности равен:
R = авс / ( 4 × √( р × ( р - а ) × ( р - в ) × ( р - с ) ) = 20 × 18 × 17 / ( 4 × √( 27,5 × ( 27,5 - 20 ) × ( 27,5 - 18 ) × ( 27,5 - 17 ) ) = 6 120 / 4 × √ ( 27,5 × 7,5 × 9,5 × 10,5 ) = 10,7 км.
Минимальное одинаковое расстояние от теннисного корта до школ А, В и С равно 10,7 км. Любое передвижение теннисного корта от этой точки О - расстояние до какой-то из школ будет уменьшаться, а до какой-то увеличиваться.