Предмет: Алгебра,
автор: masha01021
Помогите пожалуйста с решением , интеграл
Приложения:
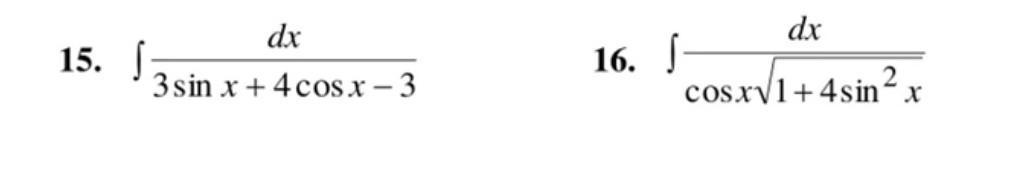
Ответы
Автор ответа:
1
ответы прикрепил на фотографии
Приложения:

masha01021:
а 16 продолжение?
вы здесь
Автор ответа:
0
Объяснение:
Упростим выражение: 3sinx+4cosx-3
Подстановка
Подстановка
а можно скриншот
вы здесь
а 16 тоже добавите
Похожие вопросы
Предмет: Русский язык,
автор: ksnsjsjnwwkjj
Предмет: Немецкий язык,
автор: beloshisdima
Предмет: Другие предметы,
автор: kimimaruyako
Предмет: Биология,
автор: arina675035
Предмет: Русский язык,
автор: vubuvhhvy