Предмет: Алгебра,
автор: nemof6073
помогите дам 30 балов срочно!!!!!!!!!!!!!
Приложения:
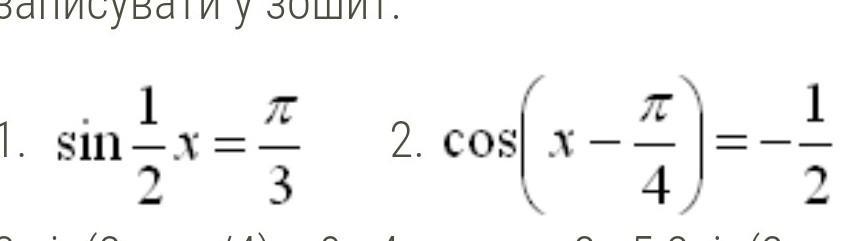
Ответы
Автор ответа:
1
Ответ:
1. решений нет. 2.
Объяснение:
1. Поскольку синус может принимать значения только из отрезка [-1;1], а π>3, то есть π/3>1, уравнение решений не имеет.
2 .
Для тех, кто знает значения косинуса только в первой четверти, а главное хочет показать, "какой он умный", приведу такое оформление решения:
veronikamila65:
здравствуйте, это снова я , можете пожалуйста решить одну пример по рядам
исправила )
Похожие вопросы
Предмет: Українська мова,
автор: roksani85
Предмет: Физика,
автор: voytushunkarina
Предмет: Қазақ тiлi,
автор: ailanamirzabekova
Предмет: Биология,
автор: kitanngorodayn
Предмет: Литература,
автор: katyayaremchuk202098