Предмет: Математика,
автор: stasik940
Доброго дня, допоможіть розв'язати ці границі. Дуже вдячний буду, якщо ще буде розписано дії розв'язання.
Приложения:
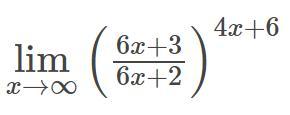
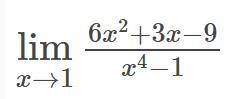
Ответы
Автор ответа:
1
Ответ:
1) Применяем 2 замечательный предел : .
2) Раскладываем многочлены на множители .
Похожие вопросы
Предмет: Математика,
автор: dilnaztop6
Предмет: Математика,
автор: gaishaalikulova207
Предмет: История,
автор: mihailickdenis
Предмет: Математика,
автор: tan09667995794