Question

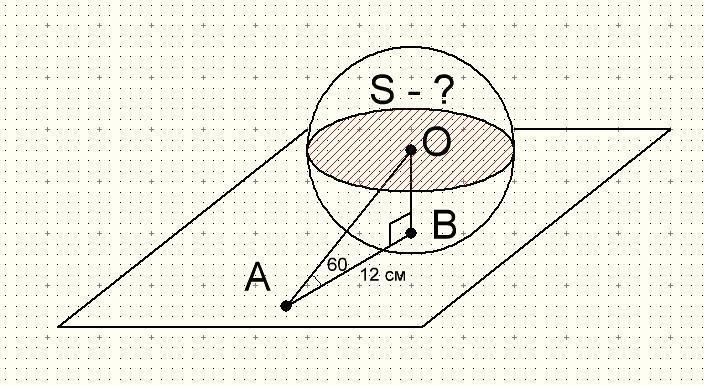
Куля, з центром в точці О дотикається до площини в точці В.
Точка А належить площині . Знайти площу діаметрального перерізу
кулі, якщо кут ОАВ дорівнює 60°, а відстань між точками А і В 12 см.

Answer 1

Ответ:

S = π*r^2 = π*(12√3)^2 = 432π см^2

Пошаговое объяснение:

Покрокове пояснення:

r = ОВ = АВ * tg(60) = 12 *√3

S = π * r² = π * (12 *√3)² = 144*3*π = 432*π см² ≈ 1357,2 см²

*******************************

Знайдемо радіус кулі.

Враховуючи, що ОВ є протилежним катетом прямокутного трикутника ОАВ до кута ОАВ 60° і катетом АВ = 12 см, за визначенням тангенсу маємо:

tg(60°) = ОВ/12

√3 = ОВ/12

ОВ = 12√3 см

Тоді радіус кулі дорівнює:

r = ОВ = 12√3 см

Знайдемо площу діаметрального перерізу кулі.

Площа діаметрального перерізу кулі дорівнює:

S = π*r^2 = π*(12√3)^2 = 432π см^2

Отже, площа діаметрального перерізу кулі дорівнює 432π см^2.