Question

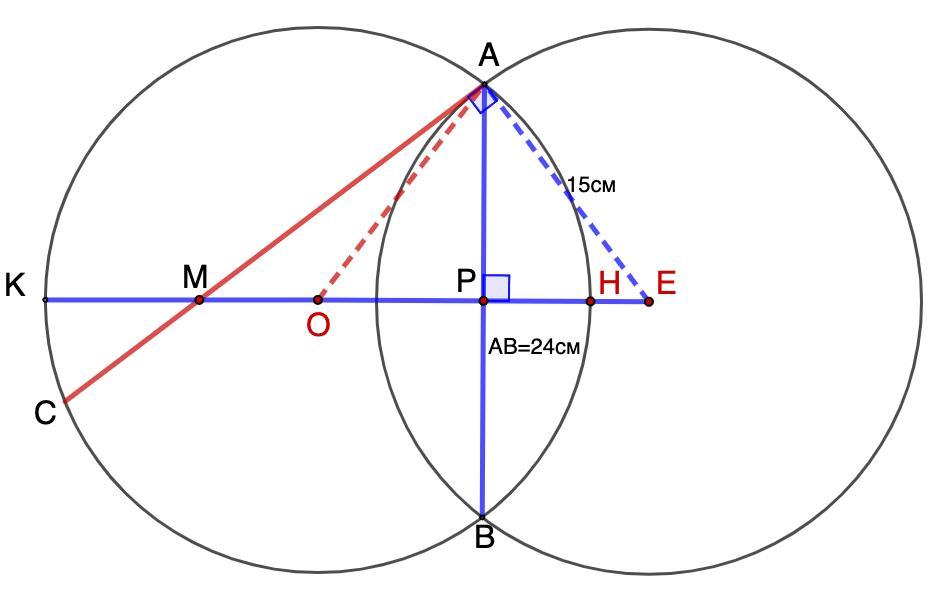
162. AB - общая хорда двух пересекающихся окруж- ностей, радиусы которых равны. Из точки А в одной ИЗ окружностей проведена хорда АС, являющаяся тельной ко второй окружности. Определить AC, если AB=24 см, а радиусы окружностей равны 15 см. каса- -​

Answer 1

Ответ:

Хорда АС равна 28,8 см.

Объяснение:

162. AB - общая хорда двух пересекающихся окружностей, радиусы которых равны. Из точки А в одной из окружностей проведена хорда АС, являющаяся касательной ко второй окружности. Определить AC, если AB=24 см, а радиусы окружностей равны 15 см.

Дано: Окр.(О,ОН) ∩ Окр.(Е,ЕА)

ОН = ЕА = 15 см;

АВ =24 см - общая хорда;

АС - касательная к Окр.(Е,ЕА);

Найти: АС.

Решение:

• Линия центров пересекающихся окружностей перпендикулярна их общей хорде и делит её пополам.

⇒ АР = РВ = 24 : 2 = 12 (см); АВ ⊥ ОЕ.

Рассмотрим ΔРАЕ - прямоугольный.

По теореме Пифагора:

РЕ² = АЕ² - АР² = 225 - 144 = 81   ⇒   РЕ = √81 = 9 (см)

Рассмотрим ΔМАЕ.

• Радиус, проведенный в точку касания перпендикулярен касательной.

⇒ ЕА ⊥ АС;  ΔМАЕ. - прямоугольный.

• Метрические соотношения в прямоугольном треугольнике:
• Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу, а квадрат катета равен произведению гипотенузы и его проекции на гипотенузу.

⇒ АР² = МР · РЕ

144 = МР · 9   ⇒   МР = 144 : 9 = 16 (см)

МА² = МР · МЕ  

МА² = 16 · (16 + 9) = 16 · 25   ⇒ МА = 4 · 5 = 20 (см)

Рассмотрим ΔОАЕ - равнобедренный (ОА = ЕА)

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ ОР = РЕ = 9 см

МО = МР - ОР = 16 - 9 = 7 (см)   ⇒   МН = МО + ОН = 7 + 15 = 22 (см)

КМ = КН - МН = 30 - 22 = 8 (см)

МА = 20 см.

Можем найти СМ.

• Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков второй хорды.

⇒ СМ · МА = КМ · МН

СМ · 20 = 8 · 22

$\displaystyle CM=\frac{8\cdot 22}{20 }=8,8\;_{(CM)}$

AC = AM + CM = 20 + 8,8 = 28,8 (см)

Хорда АС равна 28,8 см.

#SPJ1