Предмет: Алгебра,
автор: fedorowskiyarkasha
Распишите пожалуйста подробно
Приложения:
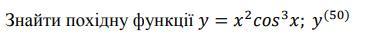
Ответы
Автор ответа:
1
Решение.
Производная произведения равна .
Производная степенной функции равна .
Похожие вопросы
Предмет: Английский язык,
автор: bogdanasaenko1
Предмет: Математика,
автор: romanblushuk
Предмет: Математика,
автор: babanazarowaaynur
Предмет: Литература,
автор: kosa13