Предмет: Математика,
автор: 1873910481903
Вычислите объем тела, образованного вращением фигуры, ограниченной графиками функций
Приложения:
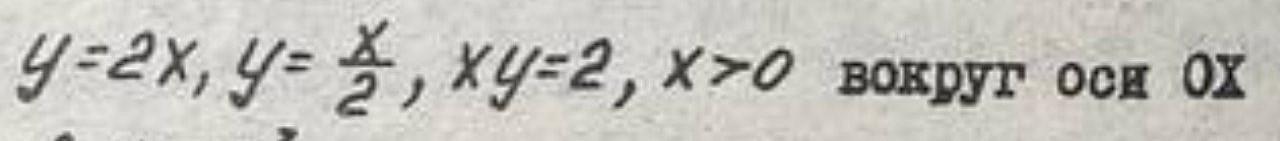
Ответы
Автор ответа:
1
Ответ:
Объём тела, образованного вращения вокруг оси ОХ криволинейной трапеции равен
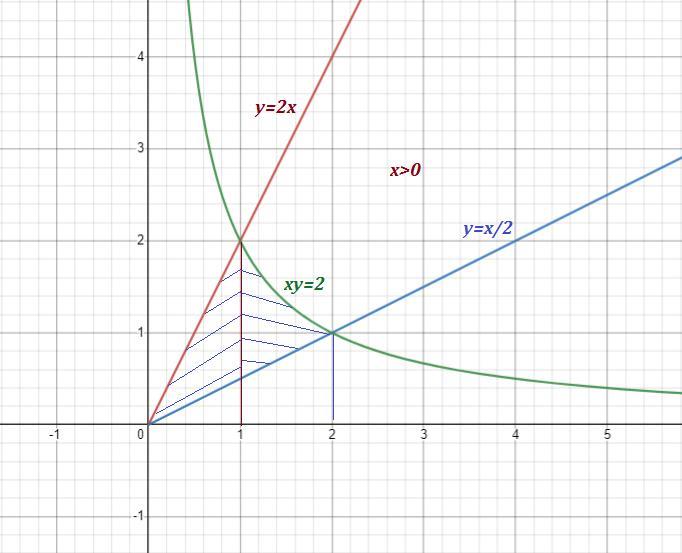
Точки пересечения графиков:
Область вращения заштрихована .
Приложения:
Похожие вопросы
Предмет: Математика,
автор: vlasovasvetlana447
Предмет: История,
автор: zanermekov7
Предмет: Химия,
автор: yegoryegor2006
Предмет: Русский язык,
автор: Polinauwulol45
Предмет: Химия,
автор: DRDeodatus