Предмет: Алгебра,
автор: fuehdaguhaeduighiu
Розв‘яжіть нерівність f’(x)>g’(x) якщо
f(x)=5x+1/x g(x)= x^3 + 1/x
Приложения:
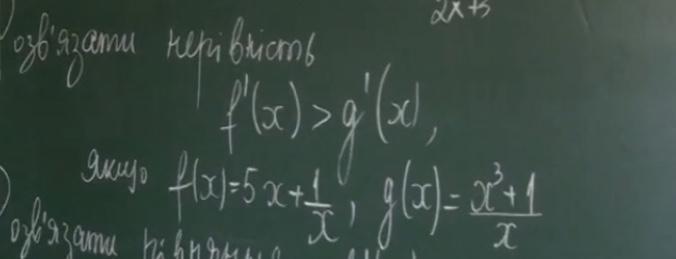
ВикаБач:
5+(1/х)' > 3x^2 +(1/x)'; 3x^2 < 5; x^2 < 5/3; -sqrt(5/3) < x < sqrt(5/3); -1.29... < x < 1.29... (а чему равно (1/x)' можно и не знать :)), оно равно -1/x^2, но в данном случае это не нужно )
.... Правда, если условие верно написано и не имелось в виду (5х+1)/x, но и в этом случае тоже не нужно. просто получится 0 > 3х^2. то есть решений нет!
Точней напиши условие! Может и g(x)=(x^3+1)/x ???
исправил
Так как g(x)=x^2 +1/x, после дифференцирования получим 5 > 2x; x < 2.5;
(1/x)' опять-таки ни вычислять ни знать не нужно!!!
Ответы
Автор ответа:
0
Объяснение:
f(x)=5x+1/x
f'(x)=5-1/(x)^2
g(x)=(x^3+1)/x
g'(x)=
x<2,5
x≠0
xє(- нескінченності;0)(0;2,5)
Зачем так сложно? Ведь g(x)=x^2 +1/x, а так как f(x)=5x+ 1/x, то производную (1/х) ни знать ни вычислять НЕ НУЖНО!
согласна
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Химия,
автор: madfenix007
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: svistunovad1302
Предмет: Алгебра,
автор: lazarevaarina2006022