Question

Фастом даб 30 баллов. Помогите дяди и тети

Answer 1

Ответ:

24

Объяснение:

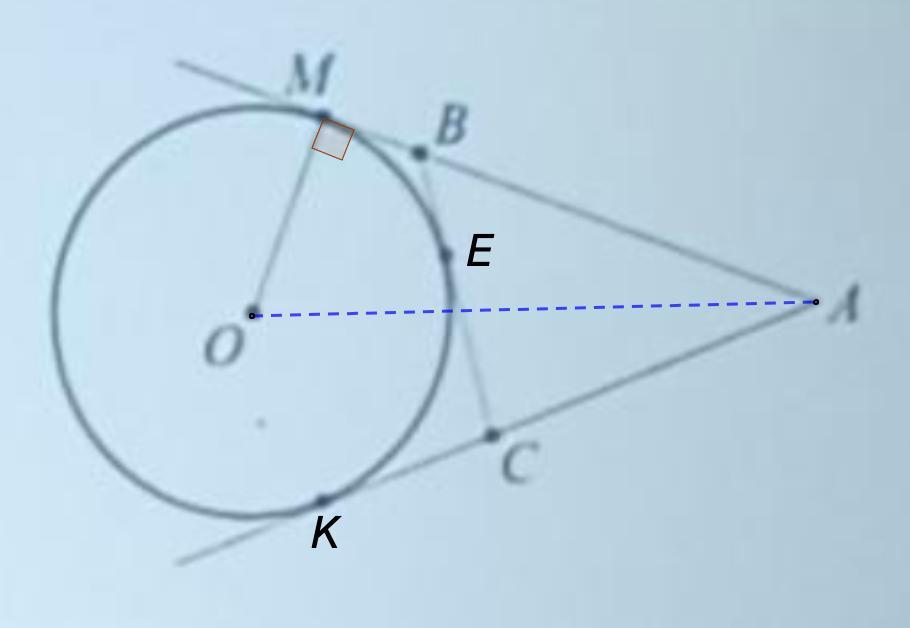
Пусть точка касания на BC это T

а на прямой АС это N

тогда AN=AM(касательные из одной точки к одной окружности)

Аналогично CN=TC; MB=BT

Найдём сторону AM по пифагору:

AM²=169-25=144

AM=AN=12

AM=AB+MB=AB+BT

AN=AC+CN=AC+CT

т.к CT+BT=CB то периметр равен сумме двух касательных AM+AN=12+12=24

Даже не дядя решил

Answer 2

Ответ:

Периметр ΔАВС равен 24 см.

Объяснение:

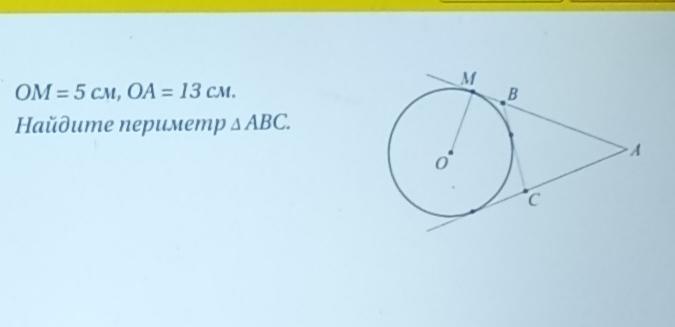
Найти периметр Δ АВС.

Дано: ∠А;

Окр.(О,ОМ) - вписанная;

ВС - касательная;

ОМ = 5 см; ОА = 13 см.

Найти: Р(ΔАВС)

Решение:

Рассмотрим ΔОМА.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒  ΔОМА. - прямоугольный.

По теореме Пифагора:

АМ² = ОА² - ОМ² = 169 - 25 = 144   ⇒   АМ = √144 = 12 (см)

• Отрезки касательных, проведенных к окружности из одной точки, равны.

⇒ АМ = АК = 12 см

ВМ = ВЕ; КС = СЕ (отрезки касательных)

Периметр - сумма длин всех сторон.

Р(ΔАВС) = АВ + ВС + АС =

= АВ + ВЕ + ЕС + АС =

= АВ + ВМ + КС + АС =

= АМ + АК = 12 + 12 = 24 (см)

Периметр ΔАВС равен 24 см.

Можно решить так, если знаете про вневписанную окружность.

Окр.(О, ОМ) - вневписанная.

• Расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением его боковой стороны равно полупериметру.

⇒ АМ = 1/2 Р(ΔАВС) = 12 (см)

Тогда Р(ΔАВС) = 12 · 2 = 24 (см)