Question

Діагоналі AC і BD трапеції ABCD (ADIIBC) перетинаються в точці O. BO : OD = 2:3,
AC =25 см. Знайдіть AO і OC.

Answer 1

Ответ:

АО=15 см, ОС=10см

Пошаговое объяснение:

Діагоналі AC і BD трапеції ABCD (ADIIBC) перетинаються в точці O. OB : OD = 2:3, AC =25 см. Знайдіть AO і OC.

Нехай маємо трапецію ABCD, AD || BC, діагоналі АС і BD перетинаються в точці О. BO:OD=2:3. AC=25см.

Розглянемо △COB і △AOD.

• ∠COB =∠AOD - як вертикальні
• ∠OCB=∠OAD - як внутрішні різносторонні кути при перетині паралельних прямих BC і AD січною АС.

Звідси слідує, що △COB ~ △AOD (за двома кутами)

З ціого слідує, що їх відповідні сторони пропорційні, тобто:

$\dfrac{CO}{AO} = \dfrac{OB}{OD}$

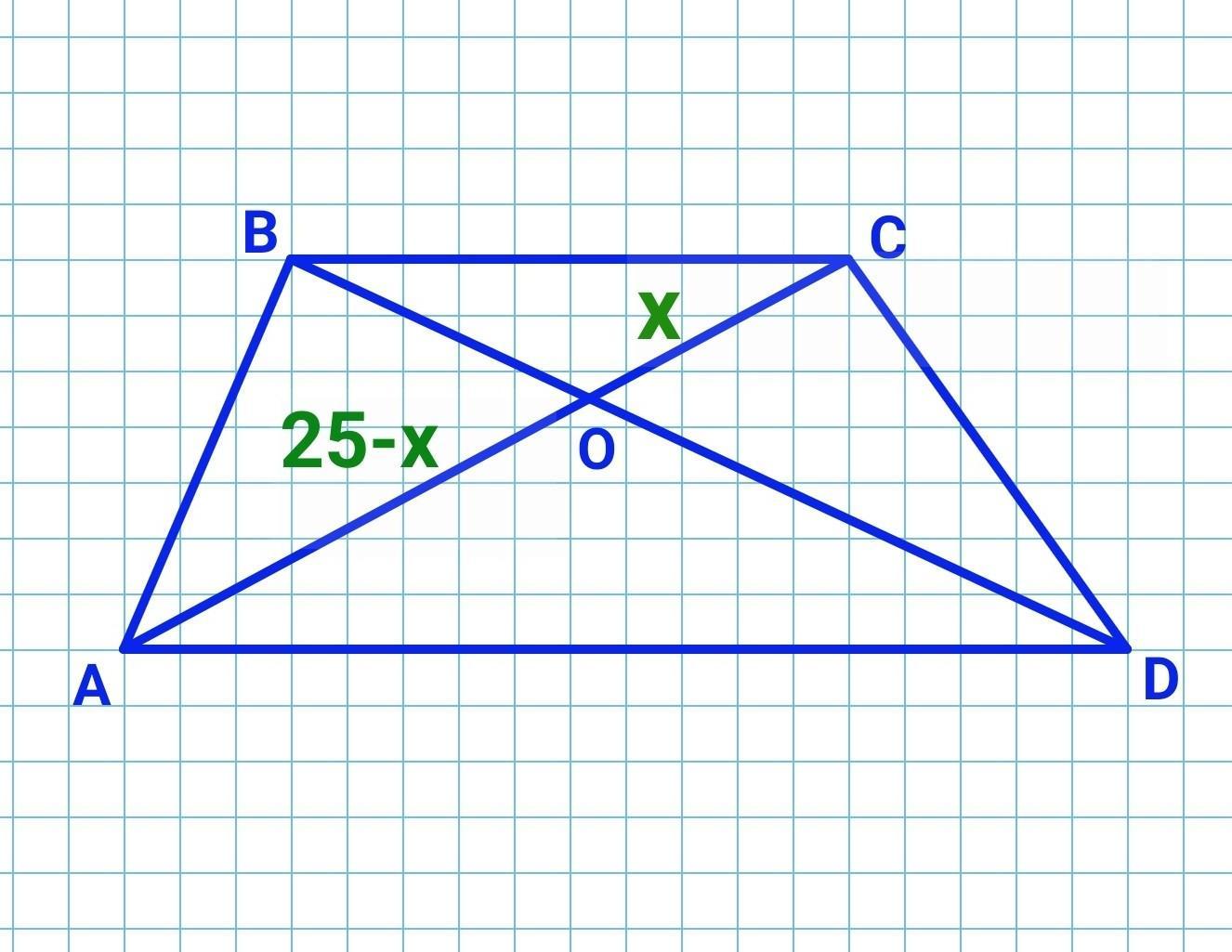
Нехай СО =x см, тоді АО=АС-СО=(25-х) см. Тоді:

$\dfrac{x}{25 - x} = \dfrac{2}{3}$

3x=50-2x

5x=50

x=10

Отже, СО=10 (см), АО=25-10= 15 (см)