Геометрия даю 100 баллов

Ответы
Ответ:
1. Диагональ правильной четырехугольной призмы равна √67 см.
2. Высота пирамиды равна 5√3 см.
Объяснение:
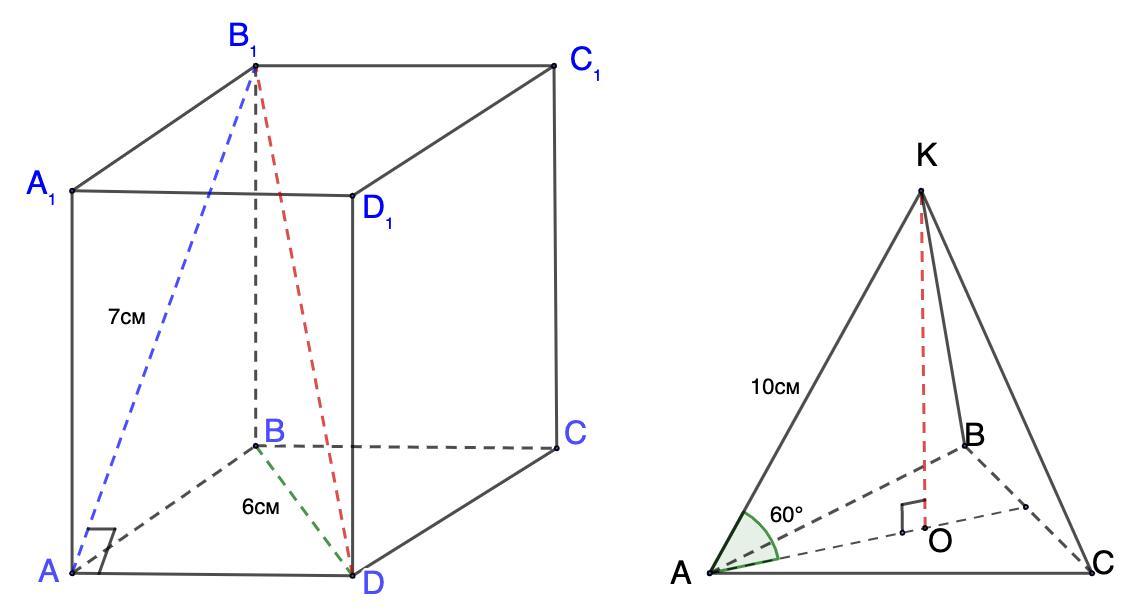
1. Найти диагональ правильной четырехугольной призмы, если диагональ ее боковой грани равна 7 см, а Диагональ основания - 6 см. 2. Боковое ребро треугольной пирамиды равно 10 см и образует с ее основанием угол 60°. Найти высоту пирамиды.
1. Дано: ABCDA₁B₁C₁D₁ - правильноая четырехугольная призма;
АВ₁ = 7 см; BD = 6 см;
Найти: В₁D.
Решение:
- В основании правильной четырехугольной пирамиды лежит квадрат.
Рассмотрим ΔАВD - прямоугольный.
Пусть АВ = AD = a
По теореме Пифагора:
AB² + AD² = BD²
2a² = 36
a² = 18
a = √18 (см)
AD ⊥ (AA₁B₁)
- Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, принадлежащей этой плоскости.
⇒ AD ⊥ AB₁.
Рассмотрим ΔАВ₁D - прямоугольный.
По теореме Пифагора:
AB₁² + AD² = B₁D²
49 + 18 = B₁D² ⇒ B₁D = √67 см
Диагональ правильной четырехугольной призмы равна √67 см.
2. Дано: КАВС - пирамида;
АК = 10 см;
угол между АК и (АВС) равен 60°;
Найти: высоту КО.
Решение:
КО ⊥ (АВС) ⇒ АО - проекция АК на (АВС)
- Угол между прямой и плоскостью равен углу между этой прямой и ее проекцией на данную плоскость.
⇒ ∠КАО = 60°
Рассмотрим ΔАКО - прямоугольный.
- Синус угла - отношение противолежащего катета к гипотенузе.
(см)
Высота пирамиды равна 5√3 см.