Предмет: Алгебра,
автор: salmantsokov2024
помогите с заданием если не сложно
Приложения:
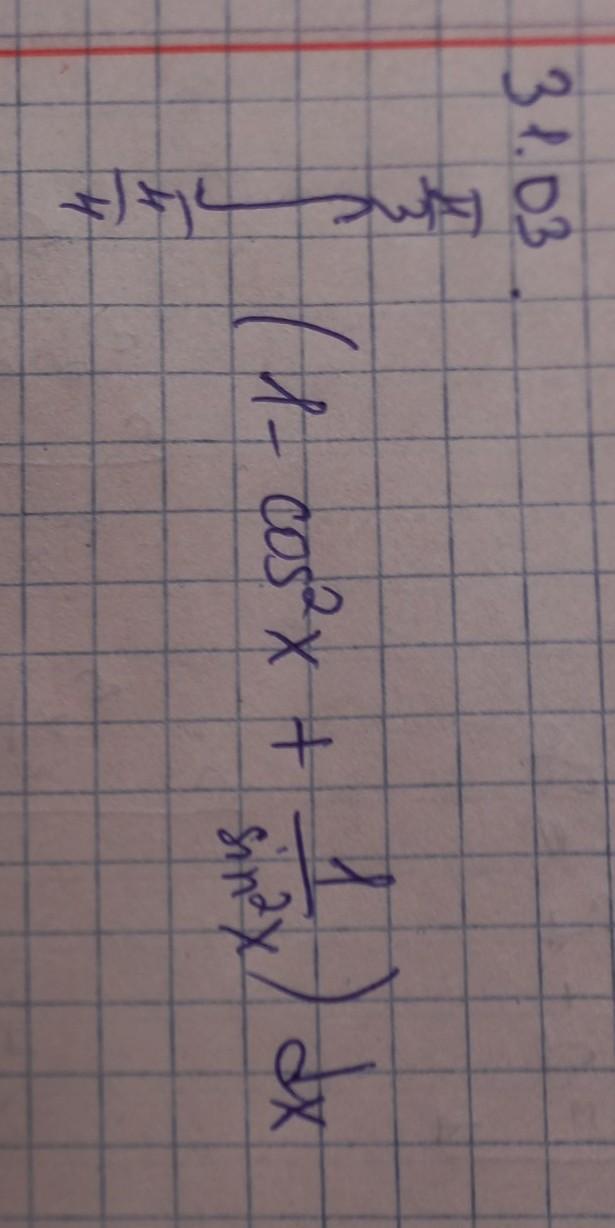
Ответы
Автор ответа:
0
Объяснение:
Похожие вопросы
Предмет: Физика,
автор: taia42
Предмет: Қазақ тiлi,
автор: natashafedorova13069
Предмет: Українська мова,
автор: Аноним
Предмет: Информатика,
автор: Аноним
Предмет: ОБЖ,
автор: nikitapetrov27