Предмет: Геометрия, автор: djdjididj

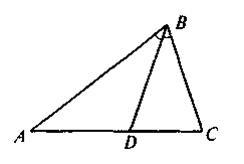
Відрізок BD — бісектриса трикутника ABC (рисунок). Площі трикутників BDC і ABC відносяться як 4 : 9. Знайдіть від­ношення АВ:ВС.

Приложения:

Ответы

Автор ответа: siestarjoki
3

Треугольники ABC и BDC имеют общую высоту из вершины B.

Площади треугольников с равными высотами относятся как основания.

S(BDC)/S(ABC) =DC/AC =4/9 => AD/DC=5/4

По теореме о биссектрисе AB/BC =AD/DC =5/4

shmel331l: В условии не сказано, что треугольники имеют общую высоту из вершины В. Так же не сказано, что они равнобедренные или равносторонние , чтобы сделать вывод, что биссектриса является высотой. Откуда вы взяли это утверждение?
siestarjoki: ABD и DBC имеют общую вершину (B) и общую прямую основания (AC). Высота - расстояние от вершины до прямой основания.
siestarjoki: биссектриса BD не является их высотой. Высота - перпендикуляр из B на прямую AC.
lera061009: почему в одинаковых заданиях разный ответ? тут 5/4 а там 9/4
Предыдущий вопрос
Следующий вопрос
Похожие вопросы
Предмет: Физика, автор: egorbugajcuk003
Автомобіль рухався з координати Х(-60) зі швидкістю 20 м/с i наздогнав велосипедиста, який почав рух з координати Х(30) зі швидкістю 12 км год. I виïхав на 0,5 години раніше. Знайти час зустрiчi пiсля виїзду автомобіля та відстані, які проїдуть автомобiль та велосипедист до зустрічі.​
1 год назад
Предмет: Биология, автор: lera915097
flestra
Задания
1) Кільчасті черви:
Кільчасті черви
а. має жалкі клітини
6. дихае зябрами
в. життєва форма полiп
г. має незамкнену кровоносну систему
Срок сдачи 2 окт
1 год назад
Предмет: Информатика, автор: sisenbaialmat
1 кол

Задание 2. Текст был составлен с использованием алфавита мощностью 32 символа и содержит

символов. Какой информационный объем в битах имеет данный текст?(2)

Решение:
1 год назад
Предмет: Алгебра, автор: nastartdasha70
Сократите дробь 16c²-8c+1/1-4c+y-4cy. В ответе должно получиться 1-4c/1+y, мне нужно именно решение.
6 лет назад
Предмет: Музыка, автор: sppdddocofo
помогите пожалуйста​
6 лет назад