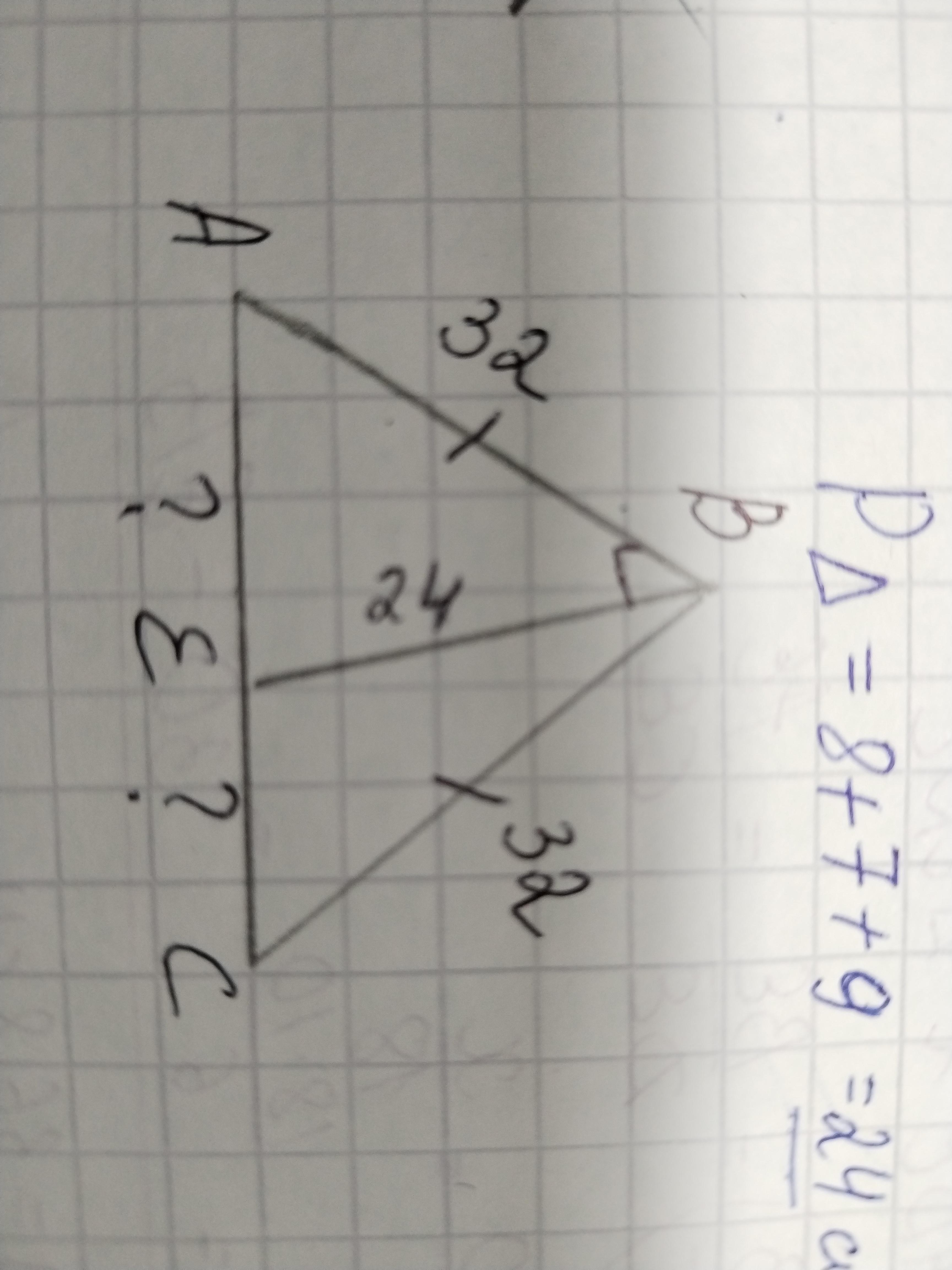
На рисунке равнобедренный треугольник ABC. AB=BC=32 см. Треугольник ABE прямоугольный. BE = 24 см. Найдите EC.
(ПОМОГИТЕ ОЧЕНЬ СРОЧНО)
Ответы
Ответ:
Пошаговое объяснение:
Сначала упростим себе вычисления, рассмотрев подобный треугольник, чьи стороны в 8 раз меньше. Главное, решив задачу для такого треугольника, не забыть ответ увеличить в 8 раз. Чтобы не менять обозначения, будем считать, что AB=BC=4, BE=3. В прямоугольном треугольнике ABE известны катеты AB=4 и BE=3, поэтому это всем известный египетский треугольник, у которого гипотенуза AE=5 (ну а кто это не знает, найдите гипотенузу по теореме Пифагора).
Далее можно идти миллионом разных способов, выберем один из них.
Пусть тогда, поскольку сумма углов в треугольнике равна 180 градусов,
По теореме синусов
Остается, возвращаясь к исходному треугольнику, результат умножить на 8.
Замечание. Нам потребовалось знание следующих результатов: теорема Пифагора (для тех, кто не знает египетский треугольник), теорема о сумме углов в треугольнике, теорема синусов, формула приведения, формула для косинуса двойного угла.
Решая другим способом, мы могли использовать теорему косинусов, решая третьим - теорему Стюарта (впрочем, я не уверен, что все знают эту замечательную теорему).
Решая четвертым способом, мы могли вообще ограничиться знанием теоремы Пифагора и определением синуса и косинуса (в этом случае нужно опустить высоту BD на сторону AC,
Снова не забываем умножить на 8.