Предмет: Геометрия,
автор: honoda20122
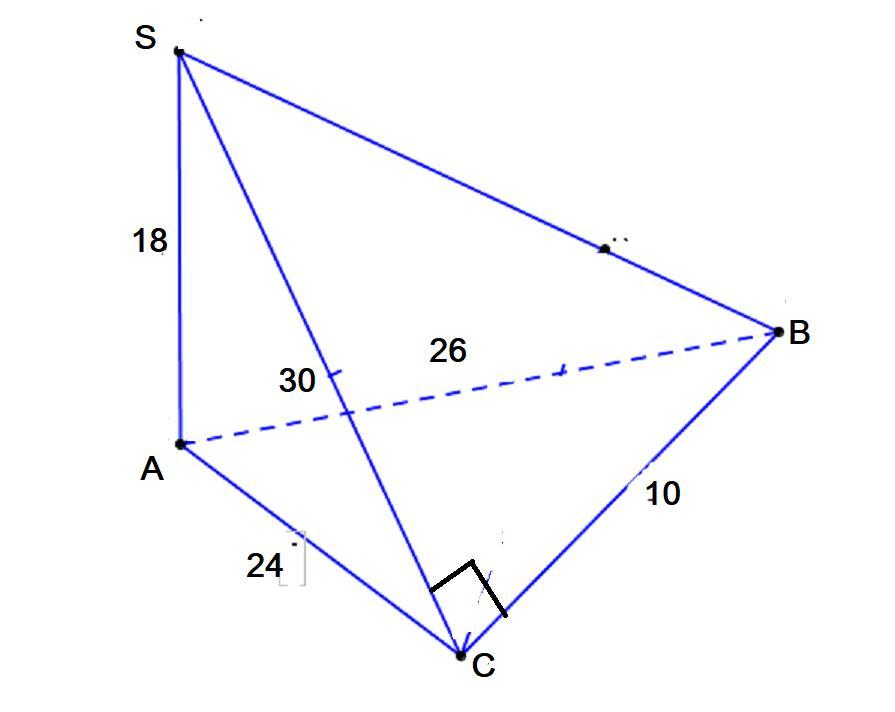
Основою піраміди с прямокутний трикутник з гіпотенузою 26 см і катетом 24 см. Ребро, що проходить через їх спільну вершину с висотою піраміди і дорівнює 18 см. Знайдіть площу бічної поверхн праміди.
Ответы
Автор ответа:
0
Имеем треугольник АВС с прямым углом С.
Находим сторону ВС основания.
ВС = √(26² - 24²) = √(676 - 576) = √100 = 10 см.
Переходим к определению площади боковой поверхности.
Площадь вертикальных граней с основаниями АВ и АС равна:
S1,2 = (1/2)*18*(26+24) = 9*50 = 450 см².
У наклонной грани угол С равен 90 градусов.
Находим длину бокового ребра, которое является высотой .
SA = √(24² + 18²) = √(576 + 324)) = √900 = 30 см.
S3 = (1/2)*10*30 = 150 см².
Ответ: Sбок = 450+150 = 600 см².
Приложения:
Похожие вопросы
Предмет: Математика,
автор: AbosrishVsolo
Предмет: Українська мова,
автор: vikusyaa20
Предмет: Геометрия,
автор: dasarosinskaa
Предмет: Математика,
автор: ursuldiana24
Предмет: Английский язык,
автор: ilona79792004