Question

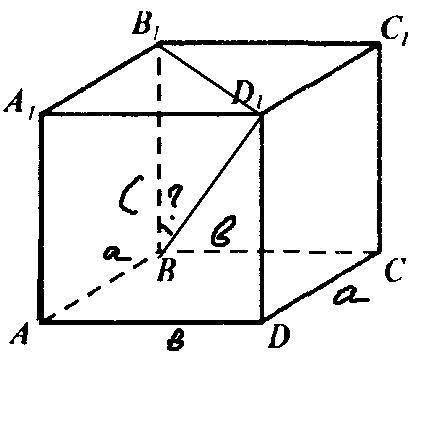
У прямокутному паралелепіпеді ABCDA1B1C1D1 AB = a, AD = b. Знайдіть відстань між прямими АА1 і BD1.

Answer 1

Ответ:

Найдем диагональ

d= Va^2+b^2

а высоту    ВВ1=С

тогда      диагонал   самого параллеппипеда   равна

D=Va^2+b^2+c^2

теперь  найдем    угол между ними

a^2+b^2=c^2+a^2+b^2+c^2-2V((a^2+b^2+c^2)*c)*cosa

-2c^2=-2V(a^2+b^2+c^2)c  * cosa

4c^4=4(a^2  +b^2+c^2)c*   cos^2a

4c^3=4(a^2+b^2+c^2)*cos^2a

cosa=V(c^3/(a^2+b^2+c^2))      где     V-кв корень  

Объяснение: