........................................................

Ответы
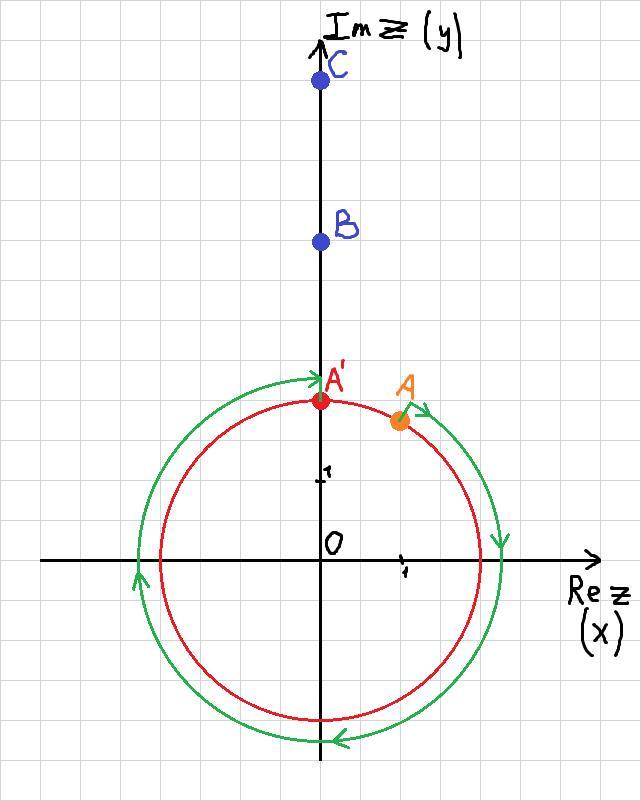
Рассмотрим числа, соответствующие заданным точкам:
Запишем число в тригонометрической форме:
Рассмотрим конечную ситуацию, когда точка повернулась на некоторый угол
. Для отличия конечную точку обозначим
.
По условию точки ,
,
лежат на одной прямой, причем
. Значит, точка
является серединой отрезка
.
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Рассмотрим точки:
Для первых координат получим:
Для вторых координат получим:
Значит, точка имеет координаты
. Соответствующее ей число:
Таким образом, при повороте точка, соответствующая числу , перешла в точку, соответствующую числу
.
Все углы поворота (угол поворота с точностью до 2п) можно найти, составив и решив уравнение:
Так как по условию угол выполнен по часовой стрелке, то есть в отрицательное направлении тригонометрической окружности, то в вышеприведенной формуле угол
вычитается из исходного аргумента (с точностью до 2п).
Останется отобрать корни на необходимом промежутке:
При :
Тот же ответ можно получить, проанализировав рисунок. Заметим, что для записанных выше чисел и
, аргумент числа
меньше аргумента числа
. Но точка, соответствующая числу
, соответствует в силу периодичности еще ряду чисел. Прибавим к аргументу числа
основной период синуса и косинуса, чтобы получить новое число, соответствующее графически той же точке, но имеющее больший аргумент:
Теперь, аргумент числа складывается из аргумента числа
и искомого угла поворота.
Найдем разность аргументов:
Ответ: 11п/6