Предмет: Алгебра,
автор: veronikamila65
Помогите пожалуйста решить , исследовать на сходимость
Приложения:
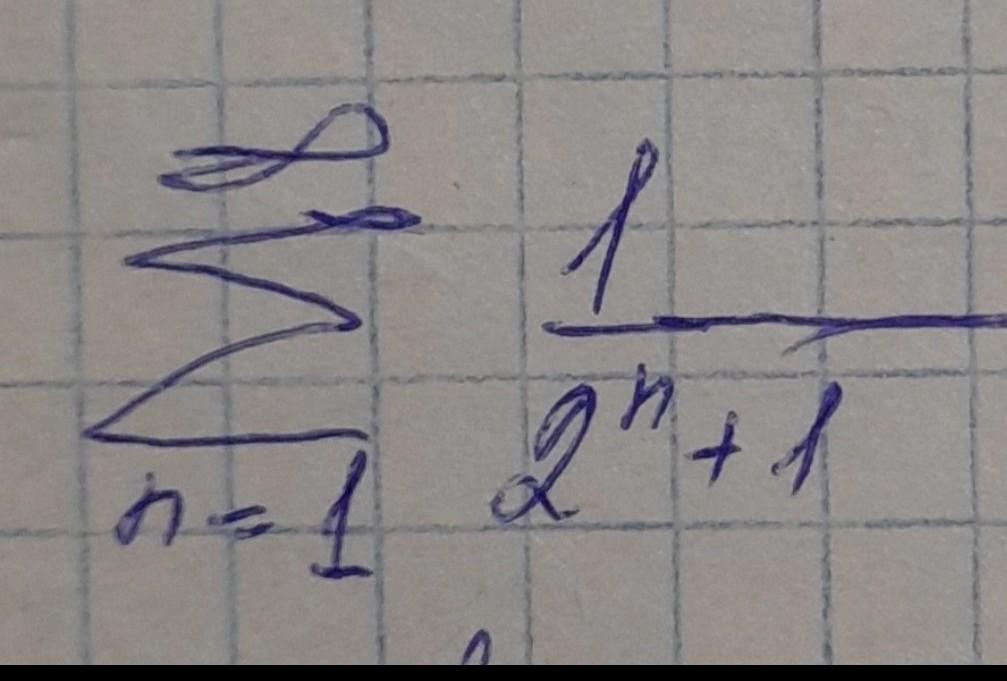
NNNLLL54:
сходится
Нет, таке не пойдет. Надо написать: исследовать на сходимость
Ответы
Автор ответа:
1
Ответ:
Сходится.
Объяснение:
Применим к ряду
. для разнообразия радикальный признак Коши:
ряд сходится, а тогда ряд
сходится по признаку сравнения.
спасибо большое
Добрый вечер! Можете пожалуйста помочь с алгеброй? Буду очень благодарна
Похожие вопросы
Предмет: Оʻzbek tili,
автор: raxnamonazirova
Предмет: История,
автор: kaznacheev0509
Предмет: Математика,
автор: m48831325
Предмет: Русский язык,
автор: ynezhenets
Предмет: Английский язык,
автор: glinskayana