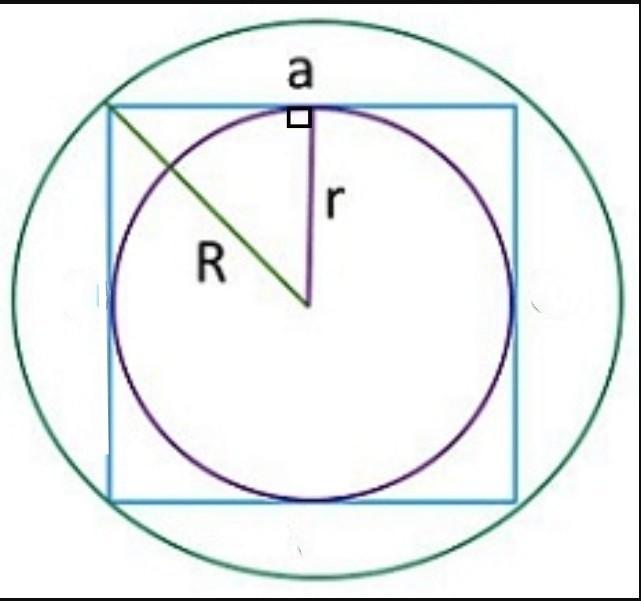
Радіус кола, описаного навколо правильного чотирикутника, дорівнює 10√2 см. Знайдіть діаметр кола, вписаного в цей чотирикутник.
Ответы
Відповідь:
Пояснення:
Позначимо сторону правильного чотирикутника через "a". Оскільки радіус кола, описаного навколо цього чотирикутника, дорівнює 10√2 см, то діаметр цього кола дорівнює 20√2 см.
З іншого боку, відомо, що радіус кола, вписаного в правильний чотирикутник, дорівнює половині діагоналі цього чотирикутника. Оскільки у правильного чотирикутника діагоналі дорівнюють одній і тій же величині, то діаметр кола, вписаного в цей чотирикутник, дорівнює добутку радіуса кола, описаного навколо цього чотирикутника, на √2:
d = 2r√2 = 2(10√2)√2 = 40 см
Отже, діаметр кола, вписаного в правильний чотирикутник, дорівнює 40 см.
Ответ:
20 см.
Объяснение:
1. По теореме сторона квадрата, вписанного в окружность радиуса R, равна а = R√2, тогда в нашем случае
а = 10√2 • √2 = 10 • 2 = 20 (см).
2. По теореме сторона квадрата, описанного около окружности радиуса r, равна а = 2r, тогда
20 = 2r.
3. Диаметр окружности d = 2r = 20 (см).