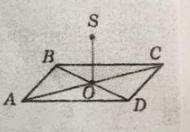
На рисунку зображено квадрат ABCD, SO L(ABC). Знайдіть відстань від точки S до точки С, якщо BD = 8 см i ΔBSD прямокутний.
Ответы
Ответ:
Оскільки ΔBSD є прямокутним, то за теоремою Піфагора ми можемо знайти довжину сторони SD за двома іншими сторонами: SD^2 = BD^2 + BS^2 Але ми не знаємо довжину сторони BS. Зверніть увагу, що ∠ASB = 90°, оскільки SO перпендикулярна до L(ABC). Тому, ΔASB також є прямокутним трикутником. Ми можемо використати теорему Піфагора для знаходження довжини сторони BS: BS^2 = AB^2 + AS^2 Зверніть увагу, що AB = BC = CD, оскільки ABCD є квадратом. Тепер, ми можемо використати відомі значення, щоб знайти відстань між точками S і C. За теоремою Піфагора, ми знаємо: SC^2 = SD^2 + DC^2 Або, використовуючи відомі значення: SC^2 = (BD^2 + BS^2) + CD^2 SC^2 = (8^2 + (AB^2 + AS^2)) + (AB^2) SC^2 = 2(AB^2) + AS^2 + 8^2 Тому, щоб знайти відстань між точками S і C, нам потрібно знайти довжину сторони AB та відстань між точками A і S. Оскільки SO є перпендикулярна до L(ABC), то точка S знаходиться на середині сторони BC, тому вона ділить сторону BC на дві рівні ділянки. Отже, AS = 1/2 BC = 1/2 BD = 4 см. Оскільки ABCD є квадратом, то AB = BC = CD = AD = BD = 8 см. Тому, за теоремою Піфагора: SC^2 = 2(8^2) + 4^2 + 8^2 = 144 SC = √144 = 12 см. Отже, відстань між точками S і C дорівнює 12 см.
Объяснение: