100 баллов!!
Задача на фото, с пояснениями и желательно с чертежом.
Спам = бан.

Ответы
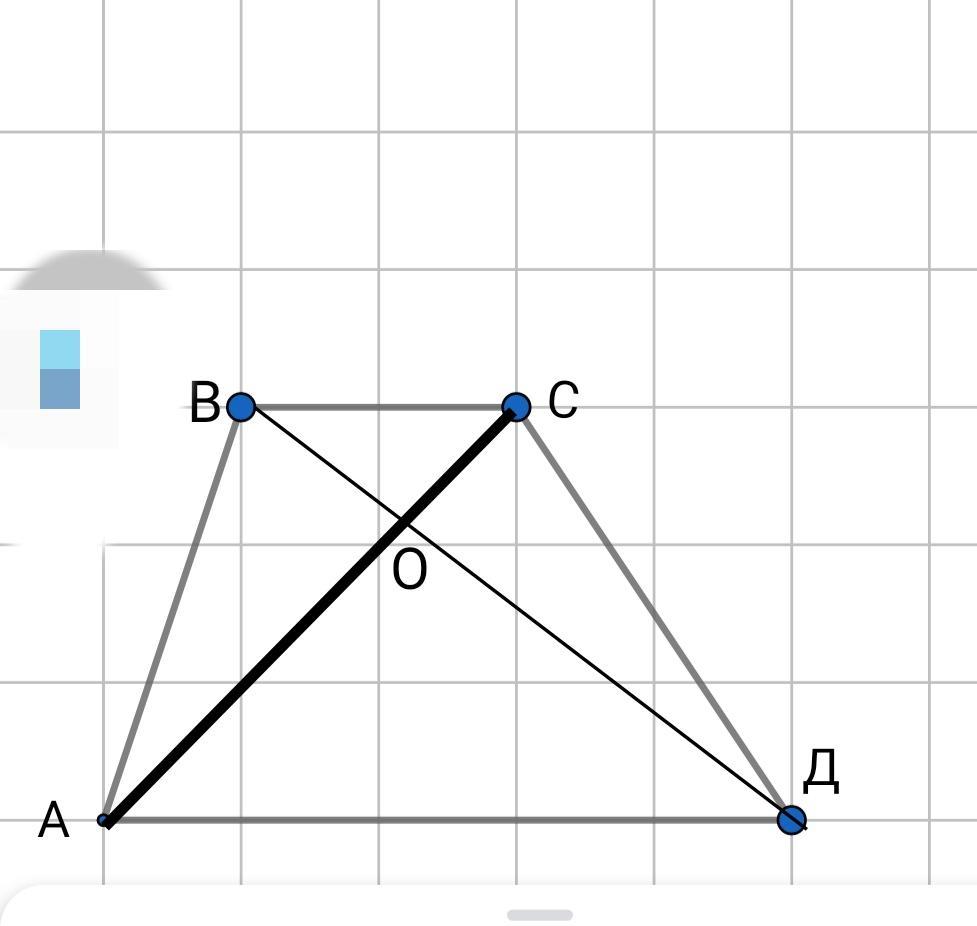
Диагонали делят трапецию на четыре треугольника. Площади треугольников, прилегающих к основаниям, равны 6 и 54. Найдите площади треугольников, прилегающих к боковым сторонам. (18; 18)
Объяснение:
1)Пусть О - точка пересечения диагоналей трапеции А ВСД. Тогда
S( AOД) =54 ед²
S( ВОС) =6 ед² .
По теореме об отношении подобных треугольников (*), имеем
к² =S(ВОС)/S(АОД)=1/9 ,
к=1/3 и отношение сходственных сторон равно 1/3 те ОС/АО=1/3,
ВО/ОД=1/3
2) Треугольники ∆АОВ, ∆СОВ имеют одинаковую высоту из точки В. Значит их площади относятся как основания
S(ВОС) /S(АОВ) =ОС/АО,
6/S(ВОС) =1/3, S(ВОС)=18 ед².
3) Треугольники ∆ВОС, ∆СОД имеют одинаковую высоту из точки С. Значит их площади относятся как основания
S(ВОС) /S(СОД) =ВО/ОД,
6/S(СОД) =1/3, S(СОД)=18 ед².
================
(*) ∆ВОС~∆АОД по 2-м углам
<ВОС=<АОД как вертикальные,
<ВСО=<ДАО как накрест лежащие при секущей АС.