Помогите пожалуйста решить задачу , исследовать на сходимость
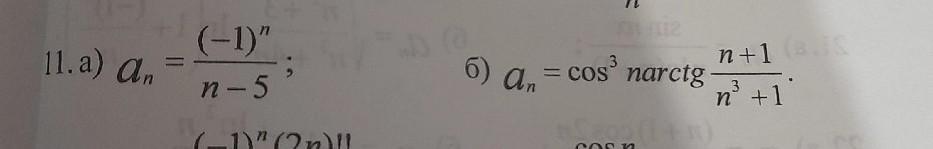
Ответы
Ответ:
а) сходится (условно); б) сходится (абсолютно).
Объяснение:
а) где
Конечно, надо рассматривать ряд
а не
поскольку не существует. Поскольку
и
ряд
по признаку Лейбница сходится.
Если (хотя в условии задачи об этом не говорится) исследовать этот ряд на абсолютную и условную сходимость, то сразу можно заметить, что ряд является гармоническим рядом и поэтому расходится. А поскольку сам ряд сходится, мы делаем вывод, что он сходится условно.
б) Сразу будем исследовать ряд на абсолютную сходимость:
Поскольку сходится как ряд Дирихле (он же обобщенный гармонический ряд)
с p=2>1, ряд
сходится по предельному признаку сравнения, а тогда ряд
сходится по тому же признаку, а тогда ряд
сходится по признаку сравнения, что означает абсолютную сходимость исходного ряда.