Розв'яжіть рівняння log4 (x+4) + log4 (1+x)=1
Ответы
Відповідь: х=0.
Пояснення: розв'язання завдання додаю
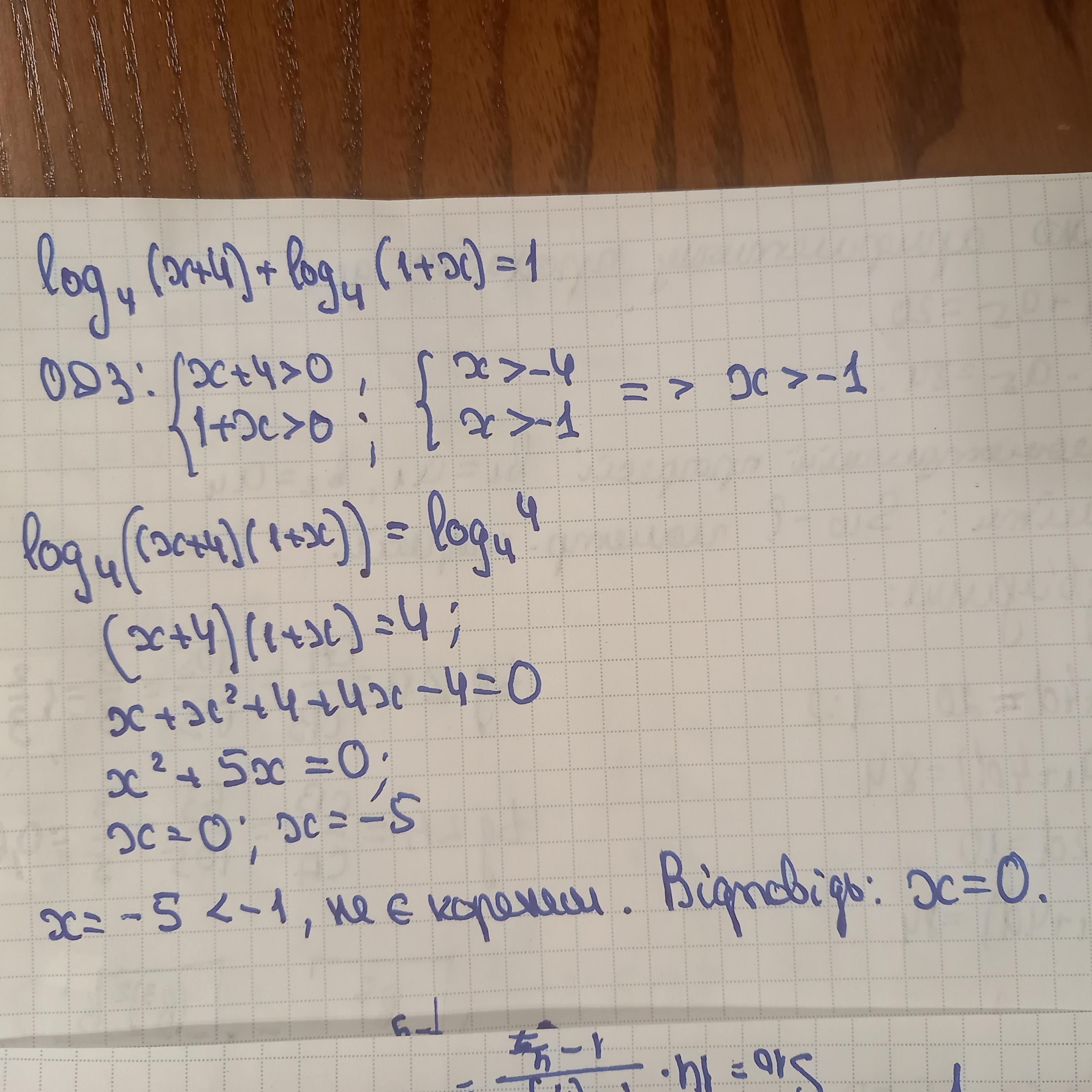
Ответ:
0.
Объяснение:
Поскольку уже есть стандартное решение, позволю себе привести другой способ.
Функции и
, стоящие в левой части уравнения, возрастают, поэтому их сумма тоже возрастает, откуда следует, что каждое своё значение она (то есть сумма) принимает ровно один раз. Подставив x=0, убеждаемся, что левая часть равна 1 (то есть равна правой части):
Итак, x=0 является решением уравнения, В силу возрастания левой части других решений быть не может.
Замечание. Возрастание логарифмической функции с основанием большим 1 можно проверить с помощью производной. Впрочем, интуитивно это и так понятно: ведь когда аргумент логарифмической функции растет, основание 4 приходится возводить во всё большую степень, чтобы получить аргумент - это мы вспомнили определение логарифма..