Срочно!!! Будь ласка! основа призми - трикутник, в якому одна сторона дорівнює 60 см, а дві інші по 90 см. бічне ребро дорівнює 120 см і утворює з площиною основи кут 45°. знайдіть ребро рівновеликого куба.
Ответы
Ответ:
Ребро куба дорівнює 60 см
Объяснение:
Основа призми - трикутник, в якому одна сторона дорівнює 60 см, а дві інші по 90 см. бічне ребро дорівнює 120 см і утворює з площиною основи кут 45°. Знайдіть ребро рівновеликого куба.
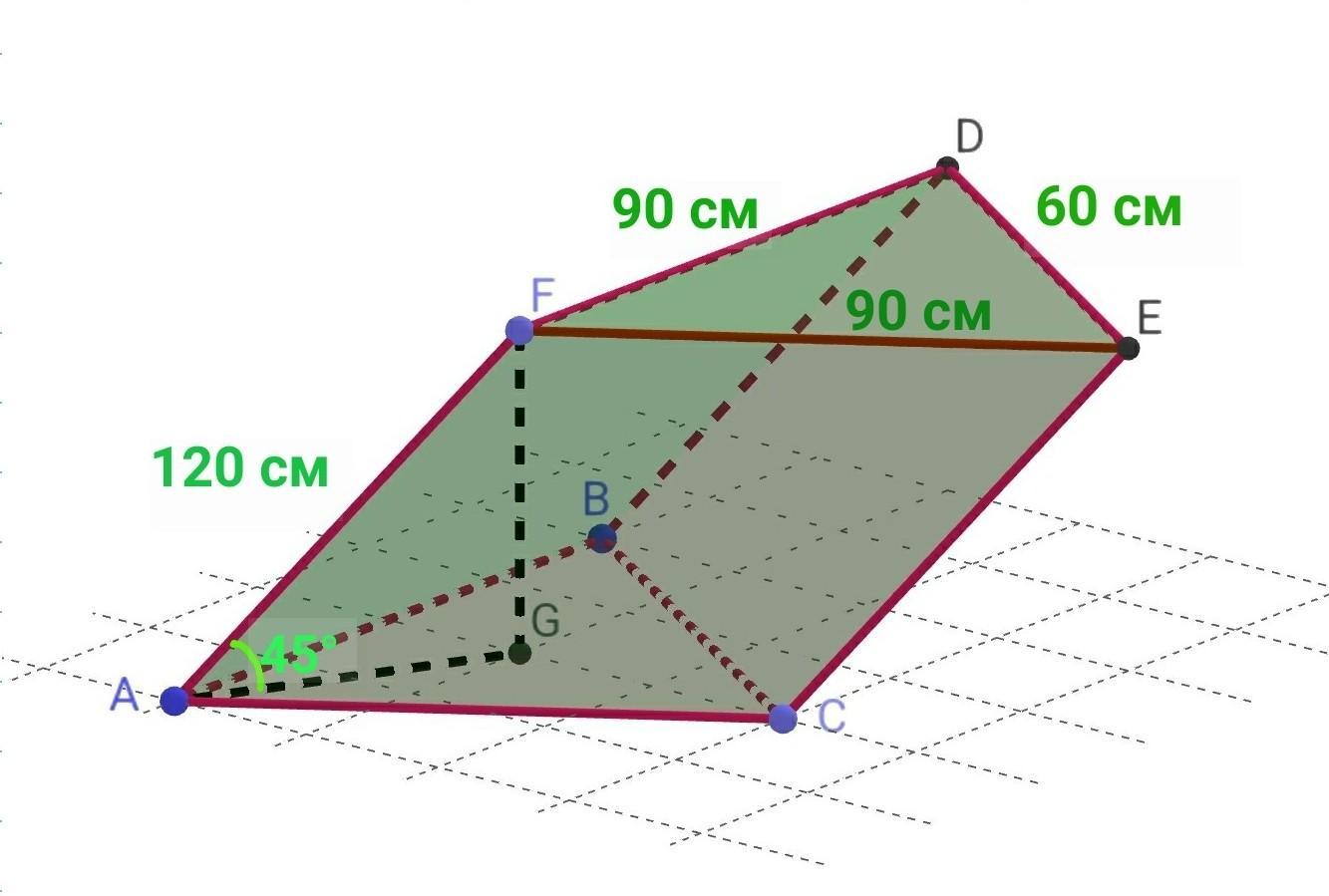
Нехай ABCFDE - задана призма, в основі якої лежить трикутник зі сторонами:
FD=FE=90 см, DE =60 см.
Бічне ребро AF=120 см.
FG - висота призми. FG⟂AG, де AG - проєкція похилої (бічного ребра AF) на площину ABC (AG ∈ABC), тому ∠FAG - кут між бічним ребром і площиною: ∠FAG=45°.
1.
У прямокутному трикутнику AGF (∠AGF=90°) відомо:
∠FAG=45°, гіпотенуза AF=120°.
За означенням синуса гострого кута прямокутного трикутника знайдемо протилежний до кута FAG катет FG (висоту призми):
звідси
(см)
2.
Площу основи призми (△FDE) знайдемо за формулою Герона.
Полуперіметр △FDE:
(см)
Тоді:
(см²)
3.
Об'єм призми дорівнює добутку площі її основи на висоту:
Маємо V=S•FG=1800√2•60√2=216000 (см³)
4.
Так як куб і призма за умовою рівновелики, то об'єм куба також дорівнює 216000 см³.
- Об'єм куба знаходять за формулою:
V=a³
де а - ребро куба.
Отже, ребро куба:
(см)
Відповідь: 60 см
#SPJ1