Предмет: Другие предметы,
автор: ilana35
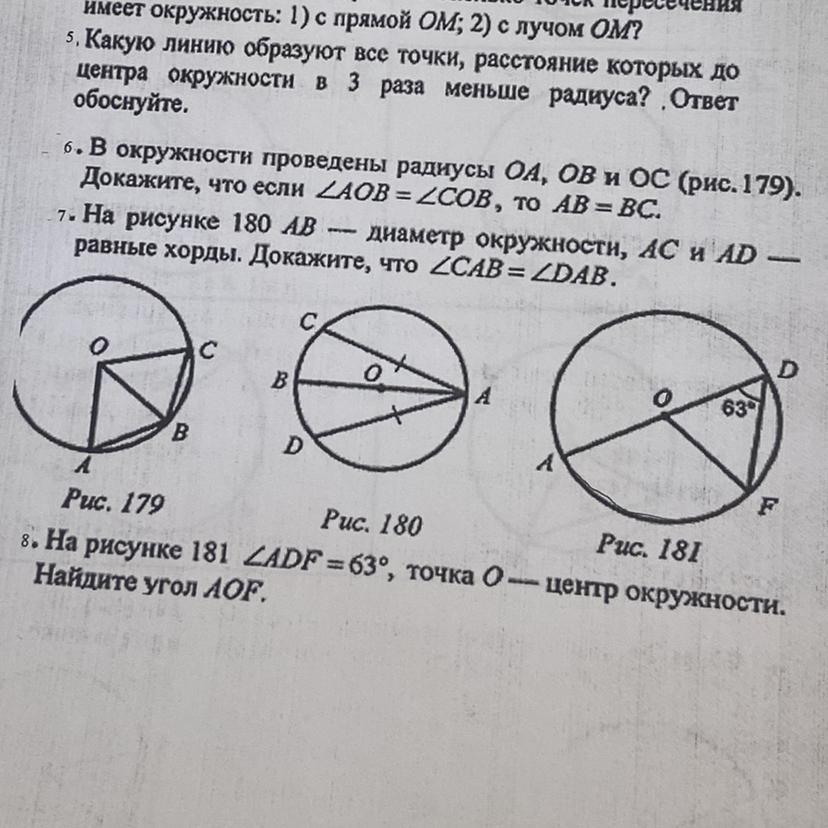
рисунке 180 AB
равные хорды. Докажите, что CAB=DAB.
0
A
Puc. 179
B
с
B
C
D
--
D..
диаметр окружности, АС и AD-
0
Dr
A
640
О
63
Ц
задание 7 ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО НУЖНО
Приложения:
Ответы
Автор ответа:
1
Ответ:
Так как BC и CD являются диаметрами окружности, то углы в прилегающих к ним точках являются прямыми углами. Таким образом, углы ACD и BCD составляют 90°. Также угол BAC равен углу BAD, так как это два соответствующих угла, соответствующих равным хордам AC и AD.
Теперь посмотрим на треугольник ABC. Так как AB и AC являются равными хордами, то углы напротив них должны быть равными - CAB=DAB.
Но угол ACD является прямым, так как CD является диаметром. Таким образом, мы видим, что CAB=DAB=90°-ACD, и это завершает доказательство.
ilana35:
СПАСИБО БОЛЬШОЕ
Похожие вопросы
Предмет: Українська література,
автор: snitkovskaana
Предмет: Немецкий язык,
автор: m6095104
Предмет: Биология,
автор: makarischuk10012010
Предмет: Английский язык,
автор: Lolfnf23
Предмет: Русский язык,
автор: Аноним