Question

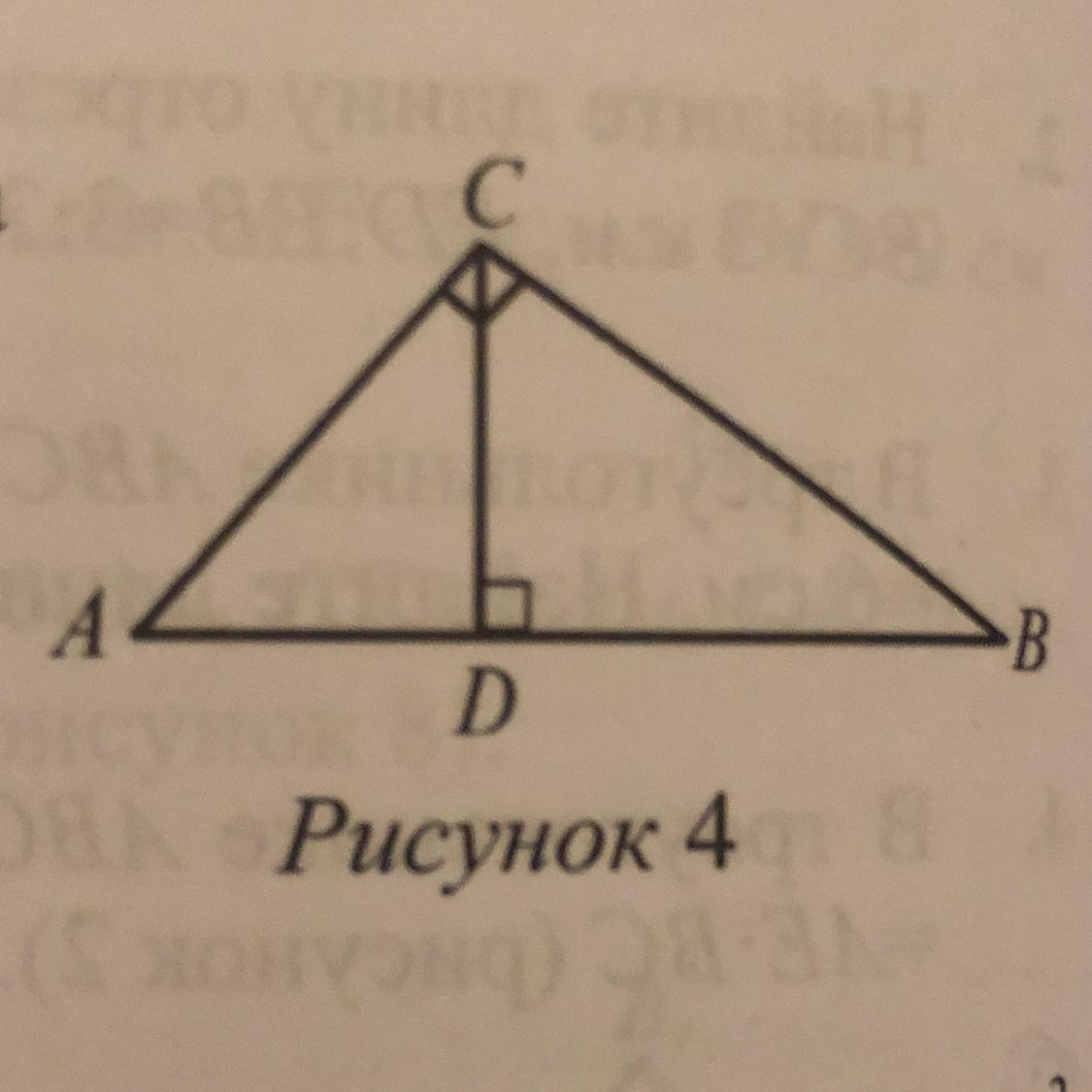
В прямоугольном треугольнике ABC с
вершины прямого угла С опущена высота
CD. Найдите площадь треугольника ABC,
если ВС=8 см, BD=4 см (рисунок 4). ДАЮ 100 баллов пжпж

Answer 1

Ответ:

32√3 cм²

Пошаговое объяснение:

Рассмотрим ΔСВD - прямоугольный, катет ВD равен половине гипотенузы ВС, значит ВD лежит против угла 30°

По теореме Пифагора СD=√(ВС²-ВD²)=√(64-16)=√48=4√3 см.

∠АСD=90-30=60°, тогда ∠А=90-60=30°, а СD - катет, лежащий против угла 30° и равный половине гипотенузы, отсюда АС=2СD=8√3 см.

По теореме Пифагора АD²=АС²-СD²=112-48=144;  АD=12 см.

АВ=12+4=16 см.

S=1/2 * 16 * 4√3 = 32√3 cм²