Question

Найдите наибольшее и наименьшее значение функции f: ​

Answer 1

Объяснение:

1.

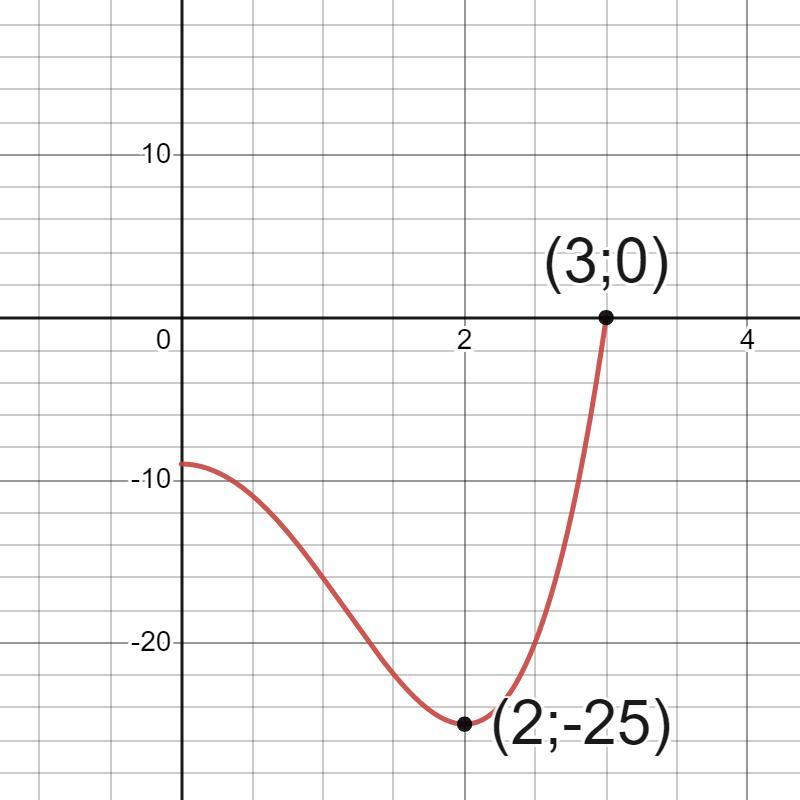
f(x)=x⁴-8x²-9 на промежутке [0;3]

1) Находим производную функции:

f'(x)=(x⁴-8x²-9)'=4x³-2*8x=4x³-16x=4x*(x^2-4)=4x*(x-2)*(x+2).

2) Приравняем производную к нулю и найдем стационарные точки;

4x*(x-2)*(x+2)=0 |:4

x*(x-2)*(x+2)=0

x=0;  x+2=0; x-2=0

x₁=0;  x₂=2;   x₃=-2.

3) Выбираем стационарные точки, которые принадлежат заданному отрезку [0;3]:

x₁=0;  x₂=2.

4) Вычиcлим значение функции на концах отрезка и в стационарных точках:

f(0)=0⁴-8*0²-9=0-0-9=-9.

f(2)=2⁴-8*2²-9=16-8*4-9=7-32=-25.

f(3)=3⁴-8*3²-9=81-8*9-9=72-72=0.

Наибольшее значение равно 0.

Наименьшее значение равно -25.

Ответ: наибольшее значение f(3)=0,

            наименьшее значение f(2)=-25.

2.

$\displaystyle\\f(x)=\frac{x^2+4}{x} \ \ \ \ [1;3]\ \ \ \ \ x\neq 0\\\\1) \ f'(x)=\frac{(x^2+4)'*x-(x^2+4)*x'}{x^2} =\frac{2x*x-(x^2+4)}{x^2} =\\\\=\frac{2x^2-x^2-4}{x^2} =\frac{x^2-4}{x^2} .\\\\2)\ \frac{x^2-4}{x^2} =0\\\\x^2-4=0\\\\(x+2)*(x-2)=0\\\\x+2=0;\ \ \ \ x-2=0\\\\x=-2;\ \ \ \ x=2.$

$3)\ x=2.$

$\displaystyle\\4)\ \\f(1)=\frac{1^2+4}{1} =\frac{1+4}{1}=5.\\\\f(2)=\frac{2^2+4}{2}=\frac{8}{2}=4.\\\\ f(3)=\frac{3^2+4}{3} =\frac{13}{3}=4\frac{1}{3}.$

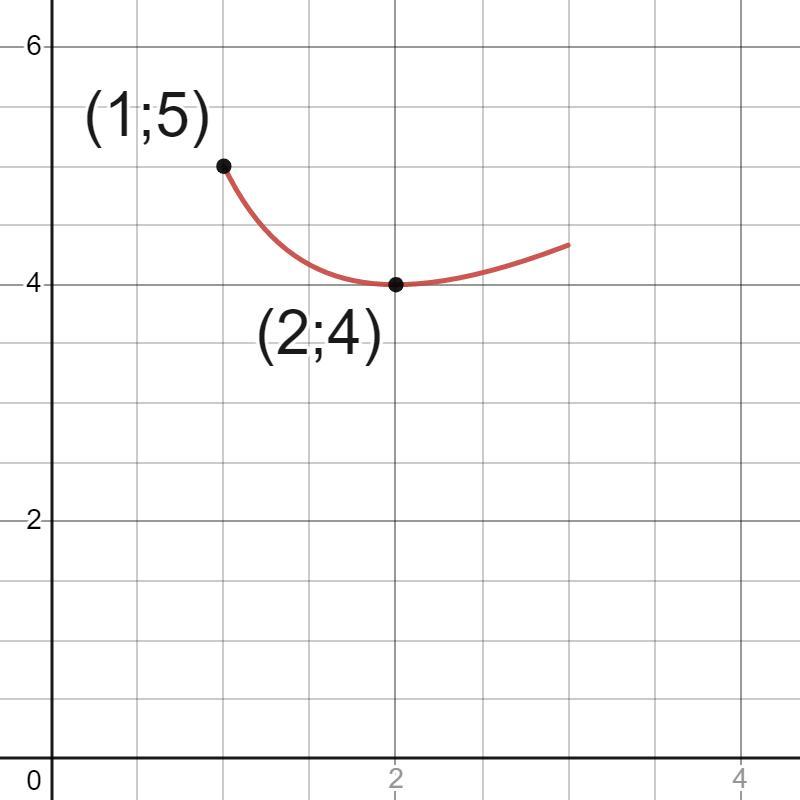
Наибольшее значение равно 5.

Наименьшее значение равно 4.

Ответ: наибольшее значение f(1)=5,

            наименьшее значение f(2)=4.

3.

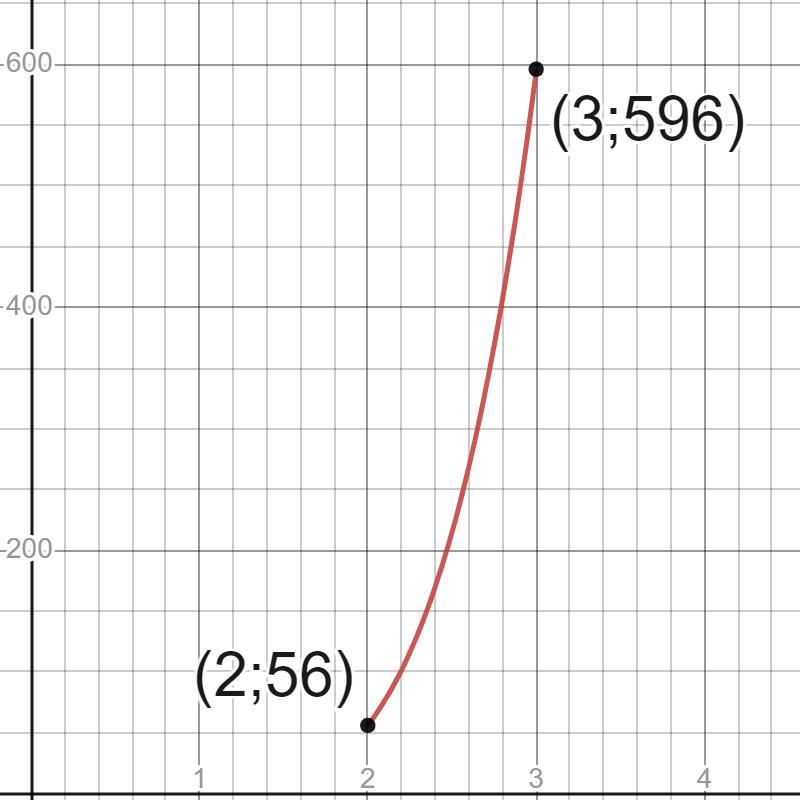
f(x)=3x⁵-5x³ на промежутке [2;3].

1) f'(x)=(3x⁵-5x³)'=5*3x⁴-3*5x²=15x⁴+15x²=15x²*(x²-1)=15x²*(x+1)*(x-1).

2) 15x²*(x+1)*(x-1)=0 |:15

x²*(x+1)*(x-1)=0

x²=0;  x+1=0;  x-1=0

x=0;    x=-1;     x=1.

3) cтационарных точек, которые принадлежат заданному отрезку [2;3], нет.

4)

f(2)=3*2⁵-5*2³=3*32-5*8=96-40=56.

f(3)=3*3⁵-5*3³==3*243-5*27=729-135=594.

Наибольшее значение равно 594.

Наименьшее значение равно 56.

Ответ: наибольшее значение f(3)=594,

            наименьшее значение f(2)=56.

4.

$\displaystyle\\f(x)=\frac{x}{x+1} \ \ \ \ \ \ [1;5]\ \ \ \ x+1\neq 0\ \ \ \ x\neq -1\\\\ 1)\ f'(x)=(\frac{x}{x+1})'=\frac{x'*(x+1)-x*(x+1)'}{(x+1)^2} =\frac{1*(x+1)-x*1}{(x+1)^2}=\\\\= \frac{x+1-x}{(x+1)^2} =\frac{1}{(x+1)^2} .\\\\2)\ \frac{1}{(x+1)^2 } \neq 0.$

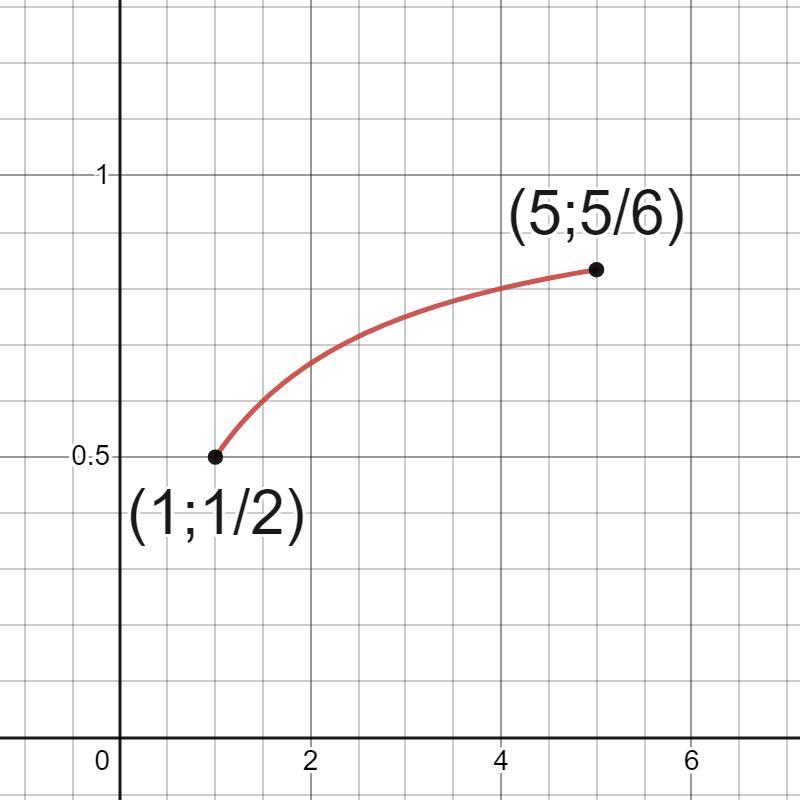
3) cтационарных точек, которые принадлежат заданному отрезку [1;5], нет.

$\displaystyle\\4)\\\\f(1)=\frac{1}{1+1}=\frac{1}{2} .\\\\\\f(5)=\frac{5}{5+1}=\frac{5}{6}$

Наибольшее значение равно 5/6.

Наименьшее значение равно 1/2.

Ответ: наибольшее значение f(5)=5/6,

            наименьшее значение f(1)=1/2.