Предмет: Алгебра,
автор: betman134
как можно быстрее дайте подробный ответ.
Приложения:
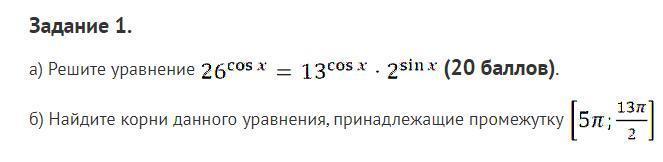
betman134:
казалось бы, 9 класс...
Ответы
Автор ответа:
2
Ответ:
Делим уравнение на
.
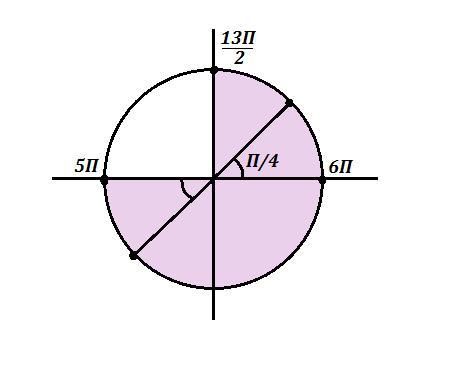
б) Корни заданного уравнения, принадлежащие промежутку
, - это
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: zajcevoleksandr44
Предмет: История,
автор: danyavovk91
Предмет: Математика,
автор: kulzanayanatt
Предмет: Математика,
автор: madikserikkan
Предмет: Математика,
автор: cubepikachu