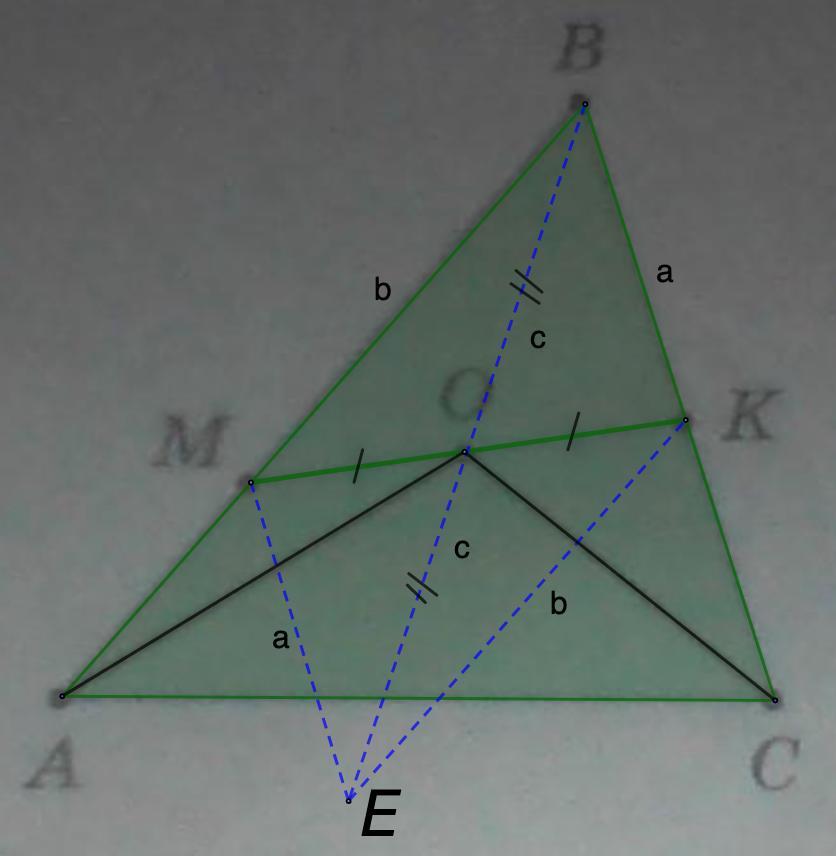
на сторонах AB и BC треугольника ABC взяли произвольные точки M и K. Точка O - середина отрезка MK. Докажите, что AM + CK < AO +CO. Срочно пж
Ответы
Ответ:
Доказано, что AM + CK < AO +CO.
Объяснение:
На сторонах AB и BC треугольника ABC взяли произвольные точки M и K. Точка O - середина отрезка MK. Докажите, что
AM + CK < AO +CO.
Дано: ΔАВС;
М ∈ АВ; К ∈ ВС;
МО = ОК.
Доказать: AM + CK < AO +CO.
Доказательство:
Соединим О и В.
- Теорема о неравенстве треугольника:
- Каждая сторона треугольника меньше суммы двух других сторон.
ΔАВО: АВ < AO + OB
ΔOBC: BC < CO + OB
Неравенства одного знака можно сложить.
AB + BC < AO + CO + 2OB
или
AM + MB + BK + KC < AO + CO + 2OB
Перенесем искомые стороны влево, остальные вправо.
AM + KC - AO - CO < 2OB - MB - BK | · (-1)
- Если обе части неравенства умножить или разделить на отрицательное число, то знак неравенства перевернется.
AO + CO - AM - KC > MB + BK - 2OB
Рассмотрим правую часть неравенства.
Все эти отрезки входят в ΔМВК.
МВ и ВК - стороны; ОВ - медиана (ОМ = ОК).
Удвоим медиану и поставим точку Е. Соединим Е с точками М и К.
МО = ОК (условие); ВО = ОЕ (построение)
- Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.
⇒ МВКЕ - параллелограмм.
- Противоположные стороны параллелограмма равны.
Пусть ЕМ = ВК = а; МВ = ЕК = b; BO = OE = c
ΔEMB: EB < EM + MB или 2с < a + b
⇒ a + b - 2c > 0 или MB + BK - 2OB > 0
- Свойство неравенств:
- Если a > b и b > 0, то a > 0
⇒ если AO + CO - AM - KC > MB + BK - 2OB и MB + BK - 2OB > 0,
то AO + CO - AM - KC > 0
⇒ AO + CO > AM + KC или AM + CK < AO +CO.
#SPJ1