Предмет: Алгебра,
автор: ivanovvictor439
упростите пожалуйста на листках или других(дам 16 баллов,ну пацаны помогите )
Приложения:
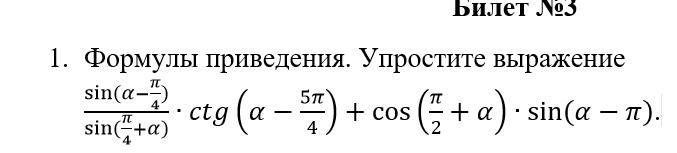
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Формулы приведения. Упростить выражение
Воспользуемся тем, что функции синус и котангенс нечетные и преобразуем к виду удобному для применения формул приведения
Воспользуемся формулами
Представим
#SPJ1
Похожие вопросы
Предмет: Английский язык,
автор: AnimeshkaMak
Предмет: Химия,
автор: kirillkikot1997
Предмет: Математика,
автор: imanasia59
Предмет: Литература,
автор: vigg43
Предмет: Математика,
автор: 7777nik