СРОЧНО ПРОШУ ВАС ОЧЕНЬ СРОЧНО
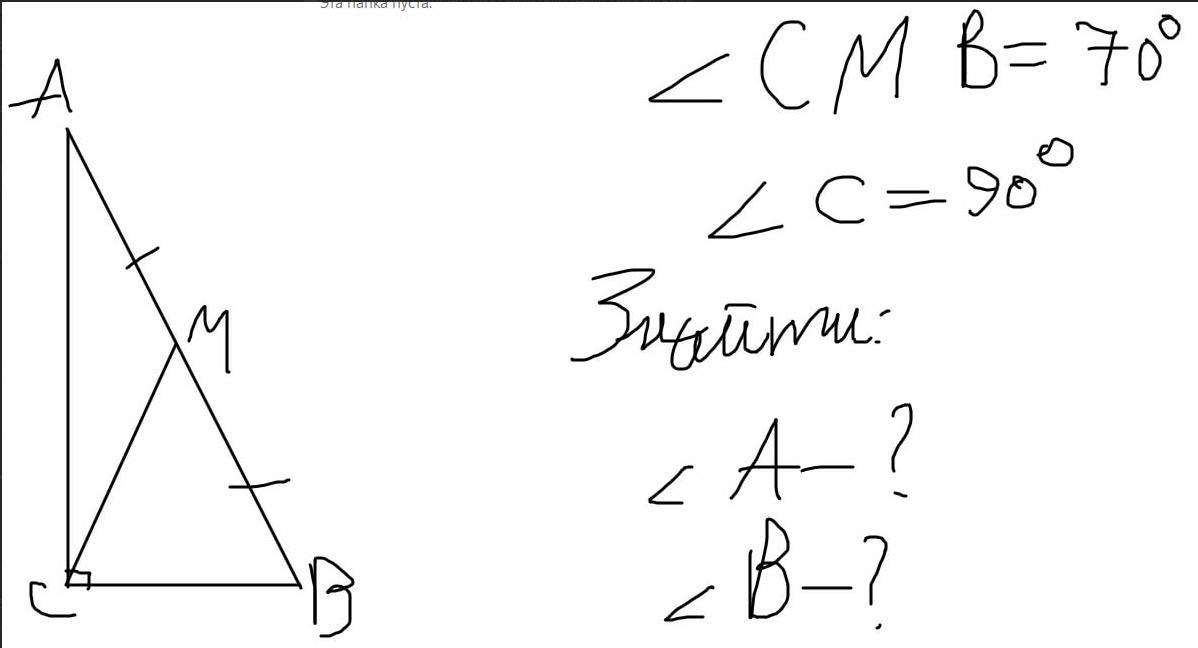
Ответы
Ответ:
1) ∠А=35°, ∠В=55°
2) довели, що ВМ - медіана
Объяснение:
1.
Дано: △АВС(∠С=90°), АМ=МВ, ∠СМВ=70°
Знайти:∠А,∠В
Розв'язання
Так як АМ=МВ, то СМ - медіана, проведена до гіпотенузи АВ.
- У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює її половині.
Тому СМ=МВ=АМ. Отже △СМВ - рівнобедрений з основою СВ.
∠МСВ=∠МВС - як кути при основі рівнобедреного трикутника.
За теоремою про суму кутів трикутника маємо:
∠МВС=МСВ=(180°-∠СМВ):2=(180°-70°):2=55°
∠В=55°
За теоремою про суму кутів прямокутного трикутника знайдемо кут А:
∠А=90°-∠В=90°-55°=35°
Відповідь: ∠А=35, ∠В=55°
2.
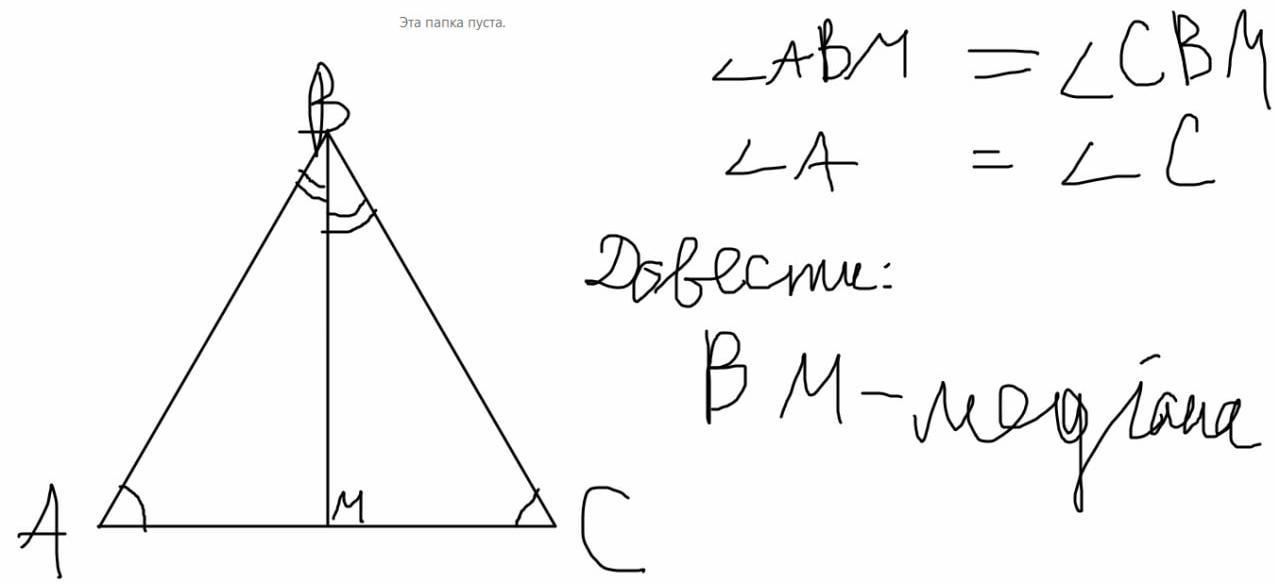
Дано: △АВС, ∠АВМ=∠СВМ, ∠А=∠С
Довести: ВМ - медіана
Доведення
За умовою ∠А=∠С, тому △АВС - рівнобедрений з основою АС (за ознакою).
- Якщо в трикутнику два кути рівні, то він рівнобедрений (ознака).
Так як ∠АВМ=∠СВМ, то ВМ - бісектриса кута АВС рівнобедреного трикутника АВС, проведена до основи.
- Бісектриса рівнобедреного трикутника, проведена до основи, є його медіаною і висотою (властивість).
Отже, ВМ - медіана △АВС (За властивістю).
Що і треба було довести.