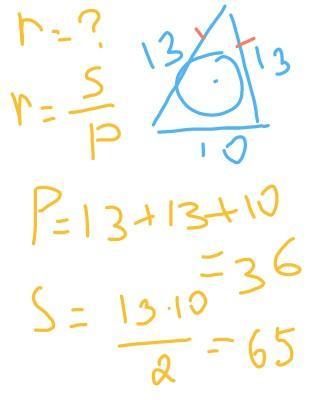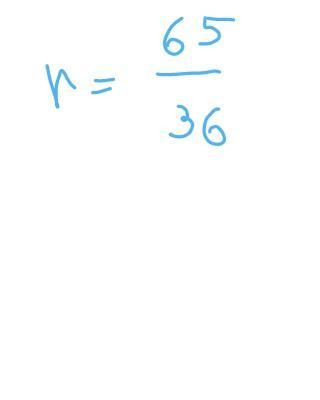2) Найдите радиус окружности, вписанной в равнобедренный тре- угольник ДАВС со сторонами АВ=BC=13, AC=10.
Ответы
Ответ: r=0,04
Объяснение:
Построим биссектрису угла DAB, которая разделит угол DAB на два равных угла, а отрезок AD разделит треугольник ДАВ на два треугольника: DAC и DAB.
Поскольку треугольник равнобедренный, то биссектриса AD и медиана DE совпадают (где E - точка пересечения биссектрисы с линией ВС).
Полупериметр треугольника ABC будет равен (13+13+10)/2 = 18.
По теореме биссектрис мы имеем соотношение:
AD/AB=CD/CB
AD/13=CD/13
AD=CD
Пусть r - радиус вписанной окружности. Тогда, по теореме:
S = pr(p-a)(p-b)(p-c) = pr^2(p-a)(p-b)(p-c)
где p = (a+b+c)/2 - полупериметр, который мы вычислили ранее.
p = (13+13+10)/2 = 18
S = r^2 * p * (p-a) * (p-b) * (p-c) = r^2 * 18 * 5 * 5 * 3 = 450r^2.
S = pr
p = 450r.
18 = 450r
r = 18/450 = 0,04.
Объяснение:
надеюсь смог вам помочь если так то можете поставить (как лучший ответ) буду рад