Найти общее решение (общий интеграл) дифференциального уравнения первого порядка 1) y'*sin^2x-ylny=0; 2)xy'+y=2y(lny-lnx); 3) (x^2+1)y'-xy=x^3+x
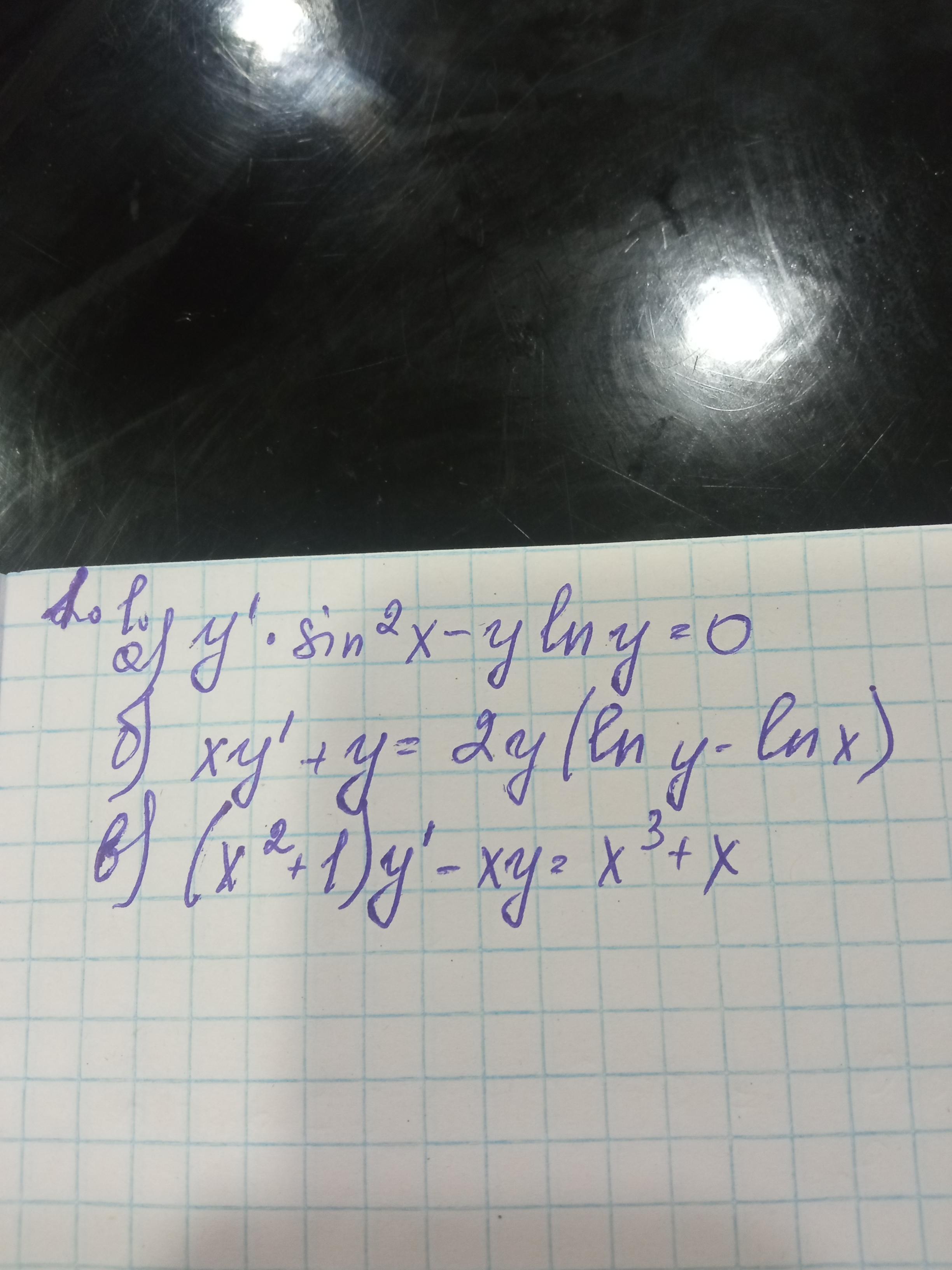
Ответы
Пошаговое объяснение:
1) y'sin^2x - ylny = 0
Для решения этого дифференциального уравнения мы можем применить метод разделяющихся переменных. Для этого выделим y' и y в левой и правой частях уравнения соответственно и разделим на y*sin^2(x):
(y'*sin^2x)/y = ln(y)/sin^2x
Заметим, что левая часть уравнения является производной (sin^2(x)*y)', а правая часть может быть переписана в виде производной логарифма:
(ln(y)/sin^2x)' = 0
Проинтегрировав это выражение, получим:
ln(y)/sin^2x = C
где C - произвольная постоянная.
Выразив y, получим общее решение исходного дифференциального уравнения:
y = e^(C*sin^2x)
2) xy' + y = 2y(ln(y) - ln(x))
Для решения этого дифференциального уравнения можно применить метод интегрирующего множителя. Уравнение можно переписать в виде:
y' + (1/x)y = 2(ln(y) - ln(x))/x
Заметим, что коэффициент при y' является функцией только от x, а коэффициент при y - функцией только от y. Поэтому мы можем умножить обе части уравнения на множитель exp(int(1/x)dx), где int(1/x)dx - интеграл от 1/x по переменной x. Получим:
exp(int(1/x)dx)*y' + (1/x)*exp(int(1/x)dx)y = 2(exp(int(1/x)dx))(ln(y) - ln(x))
Левая часть уравнения является производной (exp(int(1/x)dx)*y)', поэтому:
(exp(int(1/x)dx)y)' = 2(exp(int(1/x)dx))(ln(y) - ln(x))
Проинтегрируем обе части уравнения:
exp(int(1/x)dx)y = 2xln(y) - 2x*ln(x) + C
где C - произвольная постоянная.
Выразим y и получим общее решение дифференциального уравнения:
y = exp(-int(1/x)dx) * (C*x^2)
3. ХЗ