Question

Помогите пожалуйста
В прямоугольном треугольнике медиана проведённая к катету АС=3√7,угол A=30 градусов.Найдите АВ гипотенузу

Answer 1

Ответ:
AB=12√7

Решение:
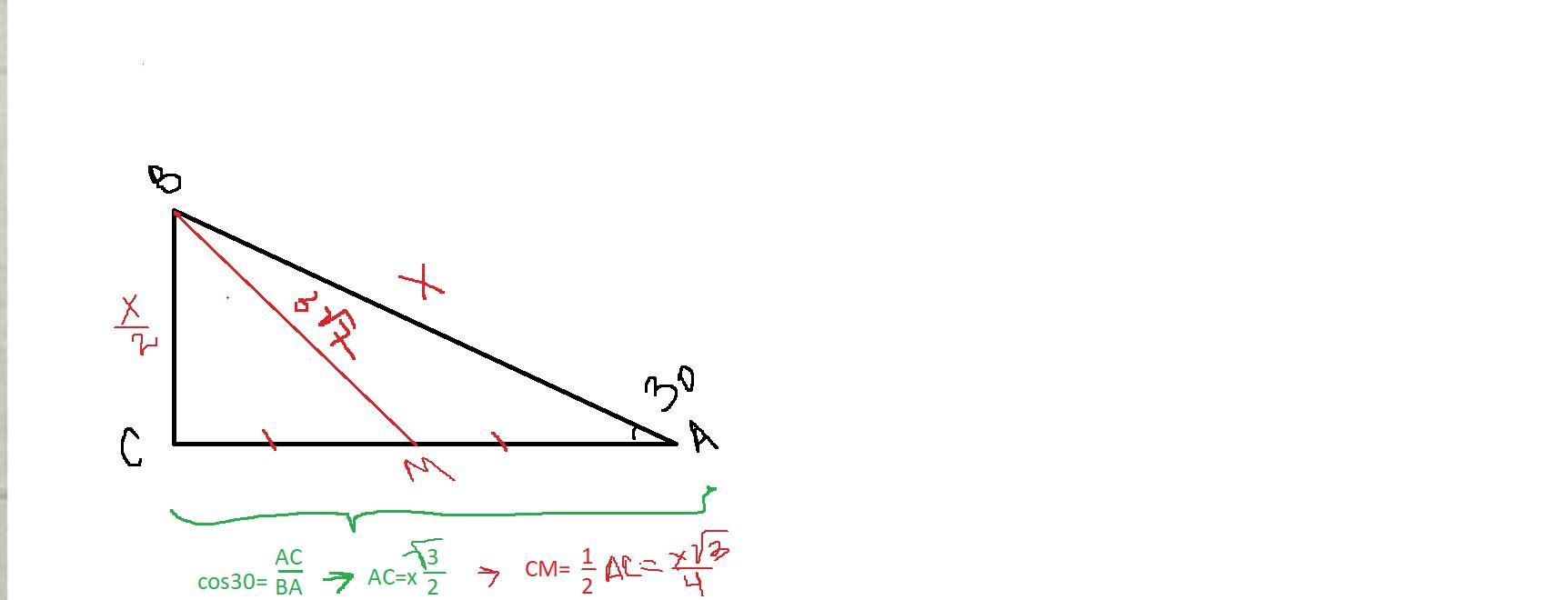
Дано: ΔАВС, С=90°; А=30°; ВМ=3√7, СМ=ВМ

Найти: АВ-?

Решение: ?

Пусть АВ =х, тогда ВС=х/2, согласно теореме о катете лежащем против угла в 30°

$cos A=\frac{AC}{AB};\\ \\AC=AB*cos A=x*\frac{\sqrt{3} }{2};$
$CM=\frac{1}{2}*AC=\frac{1}{2}*\frac{x\sqrt{3} }{2}=\frac{x\sqrt{3} }{4}$

Рассмотрим Δ ВСМ,∠С=90°, ВМ=3√7, СМ=х√3/4.
Согласно теореме Пифагора
ВМ²=СМ²+ВС²→ ВС²=ВМ²-СМ²(подставим значения вместо отрезков)

$(\frac{x}{2} )^2=(3\sqrt{7})^2- (\frac{x\sqrt{3} }{4})^2;$

$\frac{x^2}{4}=9*7-\frac{x^2*3}{16}; /*16$

4x²=63*16-3x²;

4x²-3x²=63*16;

x²=7*9*16;

$x=\sqrt{7*3^2*4^2}=3*4\sqrt{7}=12\sqrt{7}$