Предмет: Алгебра,
автор: ciellllll
Решите пожалуйста эти задание
Приложения:
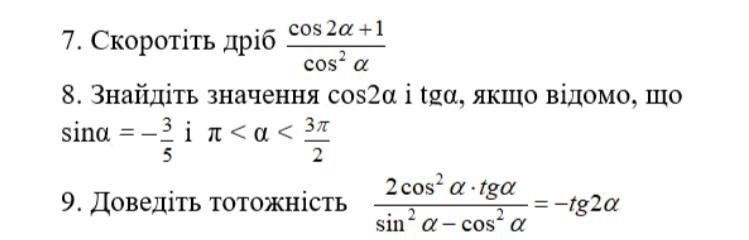
Ответы
Автор ответа:
2
Тождество доказано
Похожие вопросы
Предмет: Русский язык,
автор: mammedzadequrban99
Предмет: Русский язык,
автор: senioraaa
Предмет: Українська мова,
автор: samirkapopovic
Предмет: История,
автор: arinusy2007