Предмет: Геометрия,
автор: vikamaidanovich
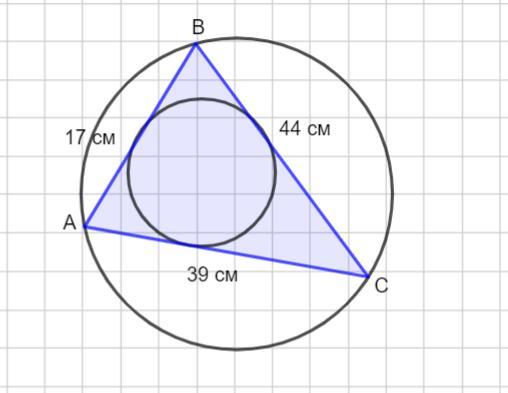
3. Знайти площу трикутника, радіуси вписаного і описаного кіл, якщо
його сторони 17см, 44см, 39см.
Ответы
Автор ответа:
1
Ответ:
S =330 см ²; r = 6,6 см; R = 22, 1 см .
Объяснение:
Найти площадь треугольника , радиусы вписанной и описанной окружностей, если его стороны равны 17 см, 44см, 39 см.
Найдем площадь треугольника по формуле Герона
где
a,b,c - стороны треугольника
Найдем полупериметр
Значит, площадь треугольника равна 330 см ².
Найдем радиус вписанной окружности по формуле
где S - площадь треугольника, P - периметр
Радиус вписанной в треугольник окружности равен 6,6 см.
Радиус, описанной около треугольника окружности, найдем по формуле
Тогда радиус описанной окружности равен 22, 1 см
Приложения:
Похожие вопросы
Предмет: Оʻzbek tili,
автор: fazylakmalov
Предмет: Русский язык,
автор: bulatbaevadinara14
Предмет: Русский язык,
автор: nastymandluk7787
Предмет: Алгебра,
автор: Аноним